




Next: DISCUSSION
Up: Fomel & Bleistein: Offset
Previous: THE KIRCHHOFF MODELING APPROXIMATION
In this section, we introduce the offset continuation partial
differential equation. We then develop its WKBJ, or ray theoretic,
solution for phase and leading-order amplitude. We explain how we
verify that the traveltime and amplitude of the integrand of the
Kirchhoff representation (4) satisfy the ``eikonal'' and
``transport'' equations of the OC partial differential equation. To
do so, we make use of relationship (15), derived from the
Kirchhoff integral.
The offset continuation differential equation derived in earlier
papers
Fomel (1994, 1995a) is
| 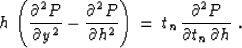 |
(16) |
In this equation, h is the half-offset (h = l/2), y is the midpoint
(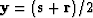 ) [hence, y = (r + s)/2],
and tn is the NMO-corrected traveltime
) [hence, y = (r + s)/2],
and tn is the NMO-corrected traveltime
| 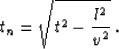 |
(17) |
Equation (16) describes the process of
seismogram transformation in the time-midpoint-offset domain. One can
obtain the high-frequency asymptotics of its solution by standard
methods, as follows.
We introduce a trial asymptotic solution of the form
| 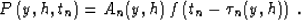 |
(18) |
It is important to remember the assumption that f is a
``rapidly varying function,'' for example, a bandlimited delta
function.
We substitute this solution
into equation (16) and collect the terms
in order of derivatives of f.
This is the direct counterpart of collecting terms in powers of
frequency when applying WKBJ in the frequency domain.
From the leading
asymptotic order (the second derivative of the function f), we
obtain the eikonal equation describing the kinematics of the OC
transformation:
| ![\begin{displaymath}
h \, \left[ {\left( \partial \tau_n \over \partial y \right)...
...ght] = \, - \, \tau_n \, {\partial \tau_n \over \partial h} \;.\end{displaymath}](img40.gif) |
(19) |
In this equation, we have replaced a multiplier of tn by
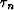 on the right side of the equation. This is consistent with
our assumption that f is a bandlimited delta function or some
equivalent impulsive source.
Analogously, collecting the terms containing the first derivative of
f leads to the transport equation describing the transformation
of the amplitudes:
on the right side of the equation. This is consistent with
our assumption that f is a bandlimited delta function or some
equivalent impulsive source.
Analogously, collecting the terms containing the first derivative of
f leads to the transport equation describing the transformation
of the amplitudes:
| 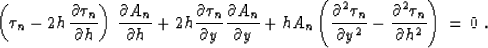 |
(20) |
We then rewrite the eikonal equation (19) in the
time-source-receiver coordinate system, as follows:
|  |
(21) |
which makes it easy (using Mathematica) to verify that the explicit
expression for the phase of the Kirchhoff integral kernel (6)
satisfies the eikonal equation for any scattering point![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
 . Here,
. Here, 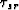 is related to
is related to 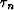 as t is related
to tn in equation (17).
as t is related
to tn in equation (17).
The general solution of the amplitude equation (20) has the
form
Fomel (1995a)
| 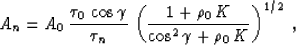 |
(22) |
where K is the reflector curvature at the reflection point. Since
the kernel (5) of the Kirchhoff integral (4)
corresponds kinematically to the reflection from a point diffractor,
we can obtain the solution of the amplitude equation for this case by
formally setting the curvature K to infinity (setting the radius of
curvature to zero). The infinite curvature transforms formula (22) to the relationship
| 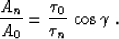 |
(23) |
Again, we exploit the assumption that
the signal f has the form of the delta function.
In this case, the amplitudes
before and after the NMO correction are connected according to the
known properties of the delta function, as follows:
| 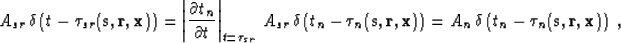 |
(24) |
with
| 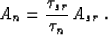 |
(25) |
Combining equations (25) and (23) yields
| 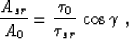 |
(26) |
which coincides exactly with the previously found formula
(15). As with the solution of the eikonal equation, we pass
from an in-plane solution in two dimensions to a solution for a
scattering point in three dimensions by replacing z2 with x22 +
z2.
It is apparent that the OC differential equation (16) and
the Kirchhoff representation have the same effect on reflection data,
because the amplitude and phase of each matches those of the other.
Thus, we see that the amplitude and phase of the Kirchhoff
representation for arbitrary offset is the point diffractor WKBJ
solution of the offset continuation differential equation. Hence, the
Kirchhoff approximation is a solution of the OC differential equation
when we hold the reflection coefficient constant. This means that the
solution of the OC differential equation has all the features of
amplitude preservation, as does the Kirchhoff representation,
including geometrical spreading, curvature effects, and phase shift
effects. Furthermore, in the Kirchhoff representation and the
solution of the OC partial differential equation by WKBJ, we have not
used the 2.5-D assumption. Therefore the preservation of amplitude is
not restricted to cylindrical surfaces as it is in Bleistein's and
Cohen's 1995 true-amplitude proof for DMO. This is what we
sought to confirm.





Next: DISCUSSION
Up: Fomel & Bleistein: Offset
Previous: THE KIRCHHOFF MODELING APPROXIMATION
Stanford Exploration Project
4/19/2000
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)