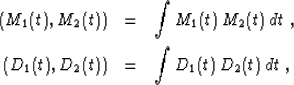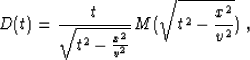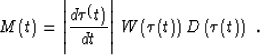Next: PULL AND PUSH NMO
Up: Fomel, Crawley & Clapp:
Previous: Introduction
In a continuous world, we could define NMO precisely as a mapping
transformation. If M(t) is a continuous zero-offset trace, and
D(t) is a trace at some non-zero offset x, then conventional NMO
with a constant velocity v is defined by the relationship
| 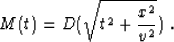 |
(1) |
If the continuous dot products in the model and data space have the
usual L2 form
| 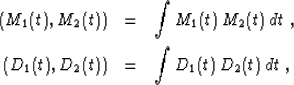 |
(2) |
| (3) |
the adjoint of operator (1) is simply
| 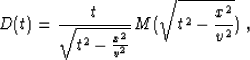 |
(4) |
where the scaling factor appears as the result of the time coordinate
stretching Crawley (1995). A generic inverse NMO
operator can be defined accordingly as
| 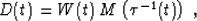 |
(5) |
where the function  defines the time coordinate transformation,
and W describes the amplitude scaling. The continuous adjoint of
(5) has the form
defines the time coordinate transformation,
and W describes the amplitude scaling. The continuous adjoint of
(5) has the form
| 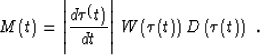 |
(6) |
The adjoint operators (5) and (6) have quite
different appearance in the discrete word of digital signal
processing. After the stretch 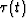 or
or 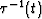 the signal
transforms from a regular grid to an irregular distribution on the
time axis. After it is interpolated back to the regular grid,
discretization errors enter the computation, and we discover that
operators (5) and (6) are no longer adjoint
to the machine precision. This fact splits the implementation of the
NMO transform into two branches: stretching and squeezing, or, as
Claerbout 1995a calls them, `` push'' and
``pull''. In some applications, only one of them is available. This
happens, for example, when the transform function
the signal
transforms from a regular grid to an irregular distribution on the
time axis. After it is interpolated back to the regular grid,
discretization errors enter the computation, and we discover that
operators (5) and (6) are no longer adjoint
to the machine precision. This fact splits the implementation of the
NMO transform into two branches: stretching and squeezing, or, as
Claerbout 1995a calls them, `` push'' and
``pull''. In some applications, only one of them is available. This
happens, for example, when the transform function 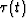 doesn't
have an easily computed inverse. In other applications, both
approaches are possible, which opens interesting possibilities for
their comparison.
doesn't
have an easily computed inverse. In other applications, both
approaches are possible, which opens interesting possibilities for
their comparison.





Next: PULL AND PUSH NMO
Up: Fomel, Crawley & Clapp:
Previous: Introduction
Stanford Exploration Project
9/12/2000