




Next: The fast marching algorithm
Up: Alkhalifah & Fomel: Fast
Previous: Introduction
Using the high-frequency approximation, wavefronts in a 3-D model can be described by
the eikonal equation,
| 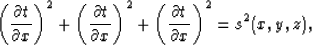 |
(1) |
where t is the traveltime, and s is the wave slowness in a 3-D model. For arbitrary slowness
models the eikonal equation is solved numerically using finite-difference schemes introduced by
Vidale (1990).
Numerically solving the eikonal equation is probably the most efficient method of obtaining wavefront
traveltimes in arbitrary velocity models. One reason for the efficiency is that we can conveniently
solve the eikonal equation over a regular grid, which eliminates the need for the interpolation commonly used with
other methods, such as
ray tracing.
A major drawback of using conventional methods to solve the eikonal equation numerically,
is that we only evaluate the fastest arrival solution,
not necessarily the most energetic Vidale (1990).
This results in less than acceptable traveltime computation
for imaging in complex media Geoltrain and Brac (1993).
Another drawback of the eikonal solvers is that the conventional
solvers are generally unstable in
complex media Popovici (1991).
Stability usually came at higher price (a finer grid) to the implementation. In addition,
conventional eikonal solvers cannot treat turning waves. Using polar
coordinates, though it does not eliminate the turning wave problem, allows for wavefronts overturning at a
considerable angle, on the condition that they do not overturn on the radial axis.
polar-dif
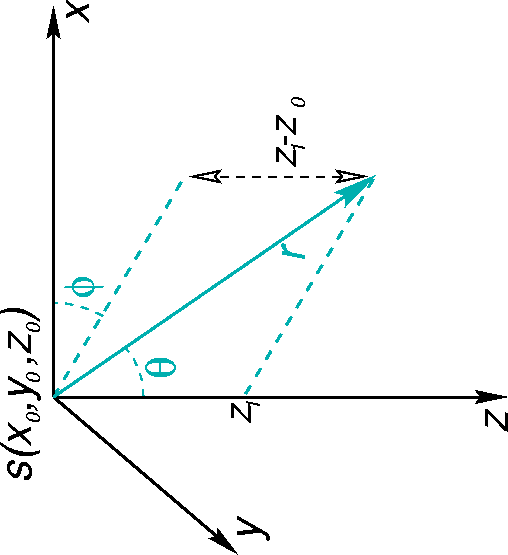
Figure 1 A spherical coordinate system given
by r, 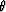 , and , and
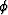 . The source, s(x0,y0,z0), is at the origin of the spherical coordinates where r=0. The
parameter r (= . The source, s(x0,y0,z0), is at the origin of the spherical coordinates where r=0. The
parameter r (=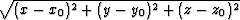 ) is the distance from the source to the
point of interest along the wavefront, which is also the magnitude of the vector. The parameter ) is the distance from the source to the
point of interest along the wavefront, which is also the magnitude of the vector. The parameter
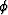 is the angle between the x-axis and the projection of the vector onto the x-y plane. The
parameter is the angle between the x-axis and the projection of the vector onto the x-y plane. The
parameter 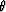 is the angle between the z-axis and the vector along a vertical plane. is the angle between the z-axis and the vector along a vertical plane.
|
|  |

The eikonal equation can also be described in spherical coordinates (r, 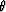 , and
, and 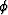 ;
see Figure 1),
as follows:
;
see Figure 1),
as follows:
|  |
(2) |
Note the  equals zero for vertical wave propagation,
which pauses a problem for this eikonal equation. However,
the change of t with respect to
equals zero for vertical wave propagation,
which pauses a problem for this eikonal equation. However,
the change of t with respect to  is, in this case, meaningless.
Therefore, a flag is necessary to remove
the
is, in this case, meaningless.
Therefore, a flag is necessary to remove
the 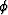 term when waves are propagating vertically or nearly vertically.
A small constant parameter (
term when waves are propagating vertically or nearly vertically.
A small constant parameter (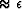 ) added to
) added to 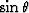 in the denominator
of the
in the denominator
of the 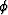 term will ensure the eikonal equation has numerical stability.
Other stability solutions are suggested by
Schneider (1993) and Fowler (1994). Also, the variation of the grid size in polar coordinates
poses a problem for
the stability of conventional solvers,
especially when encountering small scale inhomogeneities away from the source
Fowler (1994); Popovici (1991).
These stability problems are eliminated by using the fast marching method,
which is unconditionally stable.
The spherical coordinate system, as we will see later,
also helps improve the accuracy of the fast marching method.
term will ensure the eikonal equation has numerical stability.
Other stability solutions are suggested by
Schneider (1993) and Fowler (1994). Also, the variation of the grid size in polar coordinates
poses a problem for
the stability of conventional solvers,
especially when encountering small scale inhomogeneities away from the source
Fowler (1994); Popovici (1991).
These stability problems are eliminated by using the fast marching method,
which is unconditionally stable.
The spherical coordinate system, as we will see later,
also helps improve the accuracy of the fast marching method.
In polar coordinates, we eliminate the 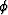 terms so that the eikonal equation,
described by r and
terms so that the eikonal equation,
described by r and 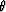 , is given by
, is given by
| 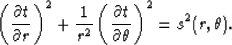 |
(3) |
The only singularity in the polar coordinate form occurs at r=0 which is easily avoidable
by placing the source at r=0, and therefore, setting the time, t, to zero at r=0.





Next: The fast marching algorithm
Up: Alkhalifah & Fomel: Fast
Previous: Introduction
Stanford Exploration Project
9/12/2000

![]() , and
, and ![]() ;
see Figure 1),
as follows:
;
see Figure 1),
as follows:
![]() terms so that the eikonal equation,
described by r and
terms so that the eikonal equation,
described by r and ![]() , is given by
, is given by