




Next: Comparison of Wilson-Burg and
Up: Theory
Previous: Minimum phase factors
The same procedure as the one described above can be applied to
cross-spectra. Let us first rewrite (1) as:
|
f(at)=s+f'(at)(at-at+1)
|
(9) |
This is clearly nothing but a first order Taylor expansion around
(s,at+1).
We can write a similar relation for a two-dimensional function as:
|
f(at,bt)=s+f(a)(at,bt)(at-at+1)+f(b)(at,bt)(bt-bt+1)
|
(10) |
where f(a) and f(b) denote the partial derivative with
respect to a and b.
If we now consider f(a,b)=ab, we can write (10) as:
|
at bt-s=bt(at-at+1)+at(bt-bt+1)
|
(11) |
Now we can again use Burg's observation (1998, personal communication)
and use (11) to factorize cross-spectra 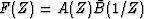 written as polynomials in
written as polynomials in 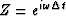 :
:
| ![\begin{displaymath}
S(Z)-A_t(Z)\bar B_t(1/Z)=
A_t( Z)[\bar B_{t+1}(1/Z)-\bar B_t(1/Z)]+
\bar B_t(1/Z)[ A_{t+1}( Z)- A_t( Z)]\end{displaymath}](img13.gif) |
(12) |
After dividing both sides by 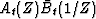 , we obtain the equation that
enables us to find both the causal and the anticausal part of a
cross-spectrum with the Wilson-Burg algorithm:
, we obtain the equation that
enables us to find both the causal and the anticausal part of a
cross-spectrum with the Wilson-Burg algorithm:
| 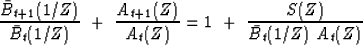 |
(13) |





Next: Comparison of Wilson-Burg and
Up: Theory
Previous: Minimum phase factors
Stanford Exploration Project
5/1/2000
![]() written as polynomials in
written as polynomials in ![]() :
: