




Next: Quadratic convergence
Up: Theory
Previous: Newton's iteration for square
Suppose now that we want to apply the same procedure to obtain the
factors of spectral functions of 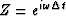 (Z-transforms). Let S(Z) be the auto-correlation that we seek to
factor into causal and anticausal parts. Burg (1998, personal
communication) recognized that we can use the Newton method to factor
(Z-transforms). Let S(Z) be the auto-correlation that we seek to
factor into causal and anticausal parts. Burg (1998, personal
communication) recognized that we can use the Newton method to factor
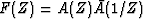 by writing an equation equivalent to
(2):
by writing an equation equivalent to
(2):
| ![\begin{displaymath}
S(Z)-A_t(Z)\bar A_t(1/Z)=
A_t( Z)[\bar A_{t+1}(1/Z)-\bar A_t(1/Z)]+
\bar A_t(1/Z)[ A_{t+1}( Z)- A_t( Z)]\end{displaymath}](img4.gif) |
(4) |
If we now divide (4) by 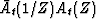 we obtain
we obtain
| 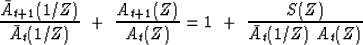 |
(5) |
Equation (5) leads to the Wilson-Burg algorithm:
- 1.
- Compute the right side of (5) by polynomial
division forwards and backwards and then add 1.
- 2.
- Abandon negative lags, to only keep the positive powers of the Z
polynomial, and also keep half of the zero lag. Now you have
At+1(Z)/At(Z).
- 3.
- Multiply out (convolve) the denominator At(Z). Now we have
the desired result At+1(Z).
Iterate as long as you wish.





Next: Quadratic convergence
Up: Theory
Previous: Newton's iteration for square
Stanford Exploration Project
5/1/2000
![]() (Z-transforms). Let S(Z) be the auto-correlation that we seek to
factor into causal and anticausal parts. Burg (1998, personal
communication) recognized that we can use the Newton method to factor
(Z-transforms). Let S(Z) be the auto-correlation that we seek to
factor into causal and anticausal parts. Burg (1998, personal
communication) recognized that we can use the Newton method to factor
![]() by writing an equation equivalent to
(2):
by writing an equation equivalent to
(2):
![]() we obtain
we obtain