




Next: Conclusions
Up: Fomel & Prucha: Angle-gather
Previous: Velocity sensitivity
As pointed out by Prucha et al. (1999), the angle gathers
can be conveniently formed in the frequency domain. This conclusion
follows from the simple formula Fomel (1996a)
| 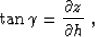 |
(15) |
where z refers to the depth coordinate of the migrated image. In the
frequency-wavenumber domain, formula (15) takes the
trivial form
| 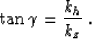 |
(16) |
It indicates that angle gathers can be conveniently formed with the help
of frequency-domain migration algorithms Stolt (1978).
This interesting opportunity requires further research.





Next: Conclusions
Up: Fomel & Prucha: Angle-gather
Previous: Velocity sensitivity
Stanford Exploration Project
5/1/2000