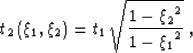Next: Operator antialiasing
Up: INTEGRAL IMPLEMENTATION OF AMO
Previous: INTEGRAL IMPLEMENTATION OF AMO
The appropriate midpoint-coordinate transformation to be applied to
the AMO impulse response is described by the following chain of
transformations
| ![\begin{displaymath}
\left[
\begin{array}
{c}
\xi_1\
\xi_2\
\end{array}...
...{array}
{c}
\Delta m_x \
\Delta m_y \end{array} \right]\;,\end{displaymath}](img29.gif) |
(5) |
where 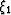 , and
, and 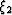 are the
transformed midpoint coordinates.
Figure
are the
transformed midpoint coordinates.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a schematic of the
relationship between the input and output offset vectors
shows a schematic of the
relationship between the input and output offset vectors  and
and
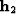 , and the transformed midpoint-coordinate unit vectors
, and the transformed midpoint-coordinate unit vectors 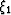 and
and 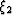 . Notice that the
. Notice that the 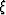 axes are dual with respect to
axes are dual with respect to
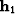 and
and 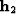 , but they define a new coordinate system for the
midpoint axes of the AMO operator. The right matrix represents a
space-invariant rotational squeezing of the coordinate, while the left
matrix is a simple rescaling of the axes by a factor dependent on the
azimuth rotation
, but they define a new coordinate system for the
midpoint axes of the AMO operator. The right matrix represents a
space-invariant rotational squeezing of the coordinate, while the left
matrix is a simple rescaling of the axes by a factor dependent on the
azimuth rotation 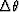 , and by the length of the dual offset
vectors. When the azimuth rotation is zero, the transformation
described in equation (5) becomes singular. In this
case the AMO operator degenerates into the 2-D offset continuation
operator, as discussed in a previous section. In practice, a simple
pragmatic method to avoid the singularity is to set a lower limit for
the product
, and by the length of the dual offset
vectors. When the azimuth rotation is zero, the transformation
described in equation (5) becomes singular. In this
case the AMO operator degenerates into the 2-D offset continuation
operator, as discussed in a previous section. In practice, a simple
pragmatic method to avoid the singularity is to set a lower limit for
the product 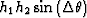 .
Because the 3-D AMO operator converges smoothly to the 2-D offset continuation
operator Fomel and Biondi (1995b), the error introduced by this
approximation is negligible.
amonewcoord
.
Because the 3-D AMO operator converges smoothly to the 2-D offset continuation
operator Fomel and Biondi (1995b), the error introduced by this
approximation is negligible.
amonewcoord
Figure 4 The geometric relationship between the unit vectors 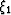 and
and 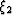 of the transformed midpoint-coordinate axes,
and the input offset
of the transformed midpoint-coordinate axes,
and the input offset 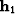 and the output offset
and the output offset 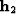 .
.

In this new coordinate system, the kinematics
of AMO are described by the following simple
relationship between the input time t1 and the
output time t2:
| 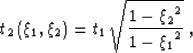 |
(6) |
and the amplitudes (based on Zhang-Black amplitudes for DMO)
are described by the following equation
| 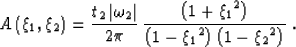 |
(7) |
Notice that this expression for the amplitudes does already take into
account the Jacobian of the transformation described in
equation (5).





Next: Operator antialiasing
Up: INTEGRAL IMPLEMENTATION OF AMO
Previous: INTEGRAL IMPLEMENTATION OF AMO
Stanford Exploration Project
6/14/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a schematic of the
relationship between the input and output offset vectors
shows a schematic of the
relationship between the input and output offset vectors