




Next: About this document ...
Up: GETTING THE WAVES FROM
Previous: Reflection seismology geometry
The remainder of chapter 8 in FGDP shows
how the algebraic techniques developed here can
be solved in reverse.
Given various waves such as the reflection data R(Z)
or the earthquake data X(Z) we may deduce
the reflection sequence
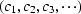 .This appears to be the solution to the practical problem.
It turns out however, for various complicated reasons,
that this does not seem to be a methodology
in widespread use in the seismic exploration business.
.This appears to be the solution to the practical problem.
It turns out however, for various complicated reasons,
that this does not seem to be a methodology
in widespread use in the seismic exploration business.
EXERCISES:
- In Figure 9 let
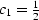 ,
, 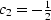 ,and
,and 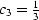 .What are the polynomial ratios T(Z) and C(Z)?
.What are the polynomial ratios T(Z) and C(Z)?
- For a simple interface,
we had the simple relations t = 1 + c, t' = 1 + c',
and c = -c'.
What sort of analogous relations can you find for the
generalized interface of Figure 9?
[For example, show 1 - T(Z)T'(1/Z) = C(Z)C(1/Z) which
is analogous to 1 - tt' = c2.]
- Show that T(Z) and T'(Z) are the same waveforms
within a scale factor.
Deduce that many different stacks of layers may have the
same T(Z).
- Consider the earth to be modeled by layers over a halfspace.
Let an impulse be incident from below (Figure 8).
Given F(Z) and G(Z), elements of the product of the layer
matrices, solve for X and for P.
Check your answer by showing that
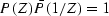 .How is X related to E?
This relation illustrates the principle of reciprocity
which says source and receiver may be interchanged.
.How is X related to E?
This relation illustrates the principle of reciprocity
which says source and receiver may be interchanged.
- Show that
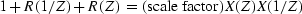 ,which shows that one may autocorrelate the transmission
seismogram to get the reflection seismogram.
,which shows that one may autocorrelate the transmission
seismogram to get the reflection seismogram.
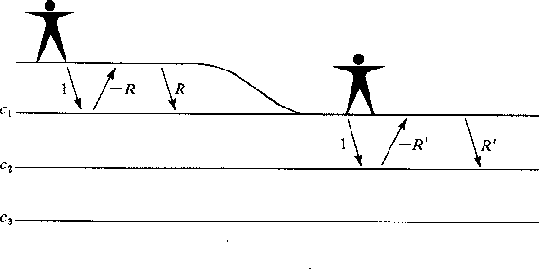
- Refer to Figure 10. Calculate R' from R.
E8-3-7
Figure 10 Stripping off the surface layer.
|
|  |






Next: About this document ...
Up: GETTING THE WAVES FROM
Previous: Reflection seismology geometry
Stanford Exploration Project
3/1/2001
![]() .This appears to be the solution to the practical problem.
It turns out however, for various complicated reasons,
that this does not seem to be a methodology
in widespread use in the seismic exploration business.
.This appears to be the solution to the practical problem.
It turns out however, for various complicated reasons,
that this does not seem to be a methodology
in widespread use in the seismic exploration business.
