




Next: SCALING THE ADJOINT
Up: Preconditioning
Previous: Three codes for inverse
Construct theoretical data with
| 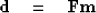 |
(30) |
Assume there are fewer data points than model points
and that the matrix 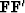 is invertible.
From the theoretical data we estimate a model
is invertible.
From the theoretical data we estimate a model 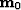 with
with
| 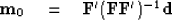 |
(31) |
To verify the validity of the estimate,
insert the estimate (31) into the
data modeling equation (30) and notice
that the estimate 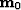 predicts the correct data.
Notice that equation
(31) is not the same
as equation (
predicts the correct data.
Notice that equation
(31) is not the same
as equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) which we derived much earlier.
What's the difference?
The central issue is which matrix of
) which we derived much earlier.
What's the difference?
The central issue is which matrix of
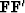 and
and
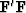 actually has an inverse.
If
actually has an inverse.
If 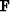 is a rectangular matrix,
then it is certain that one of the two is not invertible.
(There are plenty of real cases where neither matrix is invertible.
That's one reason we use iterative solvers.)
Here we are dealing with the case with more model points than data points.
is a rectangular matrix,
then it is certain that one of the two is not invertible.
(There are plenty of real cases where neither matrix is invertible.
That's one reason we use iterative solvers.)
Here we are dealing with the case with more model points than data points.
Now we will show that of all possible models 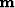 that
predict the correct data,
that
predict the correct data, 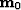 has the least energy.
(I'd like to thank Sergey Fomel for this clear and simple proof
that does not use Lagrange multipliers.)
First split (31) into an intermediate
result
has the least energy.
(I'd like to thank Sergey Fomel for this clear and simple proof
that does not use Lagrange multipliers.)
First split (31) into an intermediate
result 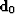 and final result:
and final result:
| 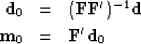 |
(32) |
| (33) |
Consider another model ( not equal to zero)
not equal to zero)
|  |
(34) |
which fits the theoretical data
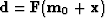 .Since
.Since
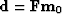 ,we see
that
,we see
that  is a null space vector.
is a null space vector.
| 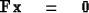 |
(35) |
First we see that 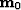 is orthogonal to
is orthogonal to  because
because
|  |
(36) |
Therefore,
| 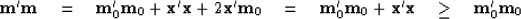 |
(37) |
so adding null space to 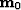 can only increase its energy.
In summary,
the solution
can only increase its energy.
In summary,
the solution
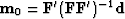 has less energy than any other model that satisfies the data.
has less energy than any other model that satisfies the data.
Not only does the theoretical solution
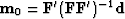 have minimum energy,
but the result of iterative descent will too,
provided that we begin iterations from
have minimum energy,
but the result of iterative descent will too,
provided that we begin iterations from 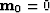 or any
or any 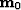 with no null-space component.
In (36) we see that the
orthogonality
with no null-space component.
In (36) we see that the
orthogonality 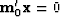 does not arise because
does not arise because 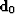 has any particular value.
It arises because
has any particular value.
It arises because 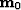 is of the form
is of the form 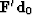 .Gradient methods contribute
.Gradient methods contribute 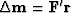 which is of the required form.
which is of the required form.





Next: SCALING THE ADJOINT
Up: Preconditioning
Previous: Three codes for inverse
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) which we derived much earlier.
What's the difference?
The central issue is which matrix of
) which we derived much earlier.
What's the difference?
The central issue is which matrix of
![]() that
predict the correct data,
that
predict the correct data, ![]() has the least energy.
(I'd like to thank Sergey Fomel for this clear and simple proof
that does not use Lagrange multipliers.)
First split (31) into an intermediate
result
has the least energy.
(I'd like to thank Sergey Fomel for this clear and simple proof
that does not use Lagrange multipliers.)
First split (31) into an intermediate
result ![]() and final result:
and final result:
![]() have minimum energy,
but the result of iterative descent will too,
provided that we begin iterations from
have minimum energy,
but the result of iterative descent will too,
provided that we begin iterations from ![]() or any
or any ![]() with no null-space component.
In (36) we see that the
orthogonality
with no null-space component.
In (36) we see that the
orthogonality ![]() does not arise because
does not arise because ![]() has any particular value.
It arises because
has any particular value.
It arises because ![]() is of the form
is of the form ![]() .Gradient methods contribute
.Gradient methods contribute ![]() which is of the required form.
which is of the required form.