




Next: norm
Up: ELIMINATING NOISE AND SHIP
Previous: Attenuation of noise bursts
As usual we
precondition by changing variables so
that the regularization operator becomes an identity matrix.
The gradient 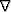 in equation (21) has no inverse, but its
spectrum
in equation (21) has no inverse, but its
spectrum 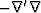 ,can be factored (
,can be factored (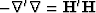 ) into triangular parts
) into triangular parts
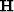 and
and 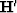 where
where 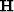 is the helix derivative.
This
is the helix derivative.
This 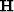 is invertible by deconvolution.
The quadratic form
is invertible by deconvolution.
The quadratic form
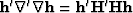 suggests the new preconditioning variable
suggests the new preconditioning variable 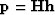 .The fitting goals in equation (21) thus become
.The fitting goals in equation (21) thus become
| 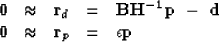 |
(22) |
with 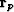 the residual for the new variable
the residual for the new variable 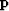 .Experience shows that an iterative solution for
.Experience shows that an iterative solution for 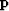 converges much
more rapidly than an iterative solution for
converges much
more rapidly than an iterative solution for 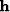 ,thus showing that
,thus showing that 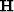 is a good choice for preconditioning.
We could view the estimated final map
is a good choice for preconditioning.
We could view the estimated final map  ,however in practice, because the depth function is so smooth,
we usually prefer to view the roughened depth
,however in practice, because the depth function is so smooth,
we usually prefer to view the roughened depth 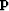 .
.
There is no simple way of knowing beforehand the best value of  .Practitioners like to see solutions for various values of
.Practitioners like to see solutions for various values of  .Practical exploratory data analysis is pragmatic.
Without a simple, clear theoretical basis, analysts
generally begin from
.Practical exploratory data analysis is pragmatic.
Without a simple, clear theoretical basis, analysts
generally begin from 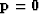 and then abandon the fitting goal
and then abandon the fitting goal
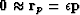 .Effectively, they take
.Effectively, they take 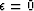 .Then they examine the solution as a function
of iteration, imagining that the solution at larger iterations
corresponds to smaller
.Then they examine the solution as a function
of iteration, imagining that the solution at larger iterations
corresponds to smaller  and that the solution at smaller iterations
corresponds to larger
and that the solution at smaller iterations
corresponds to larger  .In all our explorations, we follow this approach
and omit the regularization in the estimation of the depth maps.
Having achieved the general results we want,
we should include the parameter
.In all our explorations, we follow this approach
and omit the regularization in the estimation of the depth maps.
Having achieved the general results we want,
we should include the parameter  and adjust it until
we see a pleasing result at an ``infinite'' number of iterations.
We should but usually we do not.
and adjust it until
we see a pleasing result at an ``infinite'' number of iterations.
We should but usually we do not.





Next: norm
Up: ELIMINATING NOISE AND SHIP
Previous: Attenuation of noise bursts
Stanford Exploration Project
4/27/2004
![]() .Practitioners like to see solutions for various values of
.Practitioners like to see solutions for various values of ![]() .Practical exploratory data analysis is pragmatic.
Without a simple, clear theoretical basis, analysts
generally begin from
.Practical exploratory data analysis is pragmatic.
Without a simple, clear theoretical basis, analysts
generally begin from ![]() and then abandon the fitting goal
and then abandon the fitting goal
![]() .Effectively, they take
.Effectively, they take ![]() .Then they examine the solution as a function
of iteration, imagining that the solution at larger iterations
corresponds to smaller
.Then they examine the solution as a function
of iteration, imagining that the solution at larger iterations
corresponds to smaller ![]() and that the solution at smaller iterations
corresponds to larger
and that the solution at smaller iterations
corresponds to larger ![]() .In all our explorations, we follow this approach
and omit the regularization in the estimation of the depth maps.
Having achieved the general results we want,
we should include the parameter
.In all our explorations, we follow this approach
and omit the regularization in the estimation of the depth maps.
Having achieved the general results we want,
we should include the parameter ![]() and adjust it until
we see a pleasing result at an ``infinite'' number of iterations.
We should but usually we do not.
and adjust it until
we see a pleasing result at an ``infinite'' number of iterations.
We should but usually we do not.