




Next: LEVELED INVERSE INTERPOLATION
Up: BOTH MISSING DATA AND
Previous: Objections to interpolation error
missing data
Now let us examine the theory and coding behind the above examples.
Define a roughening filter 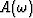 and a data signal
and a data signal 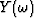 at some stage of interpolation.
The fitting goal is
at some stage of interpolation.
The fitting goal is
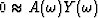 where the filter
where the filter 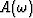 has
at least one time-domain coefficient constrained to be nonzero
and the data contains both known and missing values.
Think of perturbations
has
at least one time-domain coefficient constrained to be nonzero
and the data contains both known and missing values.
Think of perturbations 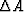 and
and 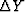 .We neglect the nonlinear term
.We neglect the nonlinear term 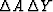 as follows:
as follows:
| 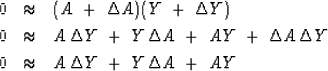 |
(37) |
| (38) |
| (39) |
Let us use matrix algebraic notation to rewrite the fitting goals
(39).
For this we need mask matrices
mask matrix
(diagonal matrices with ones on the diagonal
where variables are free and zeros where they are constrained
i.e., where 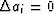 and
and 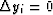 ).
The free-mask matrix for missing data is denoted
).
The free-mask matrix for missing data is denoted 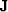 and that for the PE filter is
and that for the PE filter is 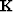 .The fitting goal (39) becomes
.The fitting goal (39) becomes
| 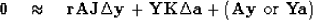 |
(40) |
Defining the original residual as
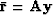 this becomes
this becomes
| ![\begin{displaymath}
\bold 0
\quad\approx\quad
\bold r \eq
\left[
\begin{array...
... y \\ \Delta \bold a
\end{array} \right]
\ +\ \bar {\bold r}\end{displaymath}](img107.gif) |
(41) |
For a 3-term filter and a 7-point data signal,
the fitting goal (40) becomes
| ![\begin{displaymath}
\left[
\begin{array}
{cccccccccc}
a_0& . & . & . & . & . &...
...r r_7 \\ \bar r_8
\end{array} \right]
\quad \approx \ \bold 0\end{displaymath}](img108.gif) |
(42) |
Recall that
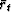 is the convolution of at with yt,
namely,
is the convolution of at with yt,
namely,
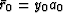 and
and
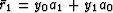 , etc.
To optimize this fitting goal we first initialize
, etc.
To optimize this fitting goal we first initialize
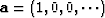 and then put zeros in for missing data in
and then put zeros in for missing data in 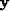 .Then we iterate over equations (43) to (47).
.Then we iterate over equations (43) to (47).
| 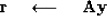 |
(43) |
| ![\begin{displaymath}
\left[
\begin{array}
{c}
\Delta \bold y \\ \Delta \bold a...
...\bold A' \\ \bold K' \bold Y'
\end{array} \right]
\
\bold r\end{displaymath}](img114.gif) |
(44) |
| ![\begin{displaymath}
\Delta \bold r
\quad\longleftarrow\quad
\left[
\begin{arr...
...ay}
{c}
\Delta \bold y \\ \Delta \bold a
\end{array} \right]\end{displaymath}](img115.gif) |
(45) |
| 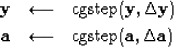 |
(46) |
| (47) |
This is the same idea as all the linear fitting goals we have been solving,
except that now we recompute
the residual  inside the iteration loop
so that as convergence is achieved (if it is achieved),
the neglected nonlinear term
inside the iteration loop
so that as convergence is achieved (if it is achieved),
the neglected nonlinear term 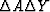 tends to zero.
tends to zero.
My initial research proceeded by linearization like (39).
Although I ultimately succeeded,
I had enough difficulties that
I came to realize that linearization is dangerous.
When you start ``far enough'' from the correct solution
the term 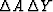 might not actually be small enough.
You don't know how small is small,
because these are not scalars but operators.
Then the solution may not converge to the minimum you want.
Your solution will depend on where you start from.
I no longer exhibit the nonlinear solver missif
until I find a real data example where it produces noticibly better results
than multistage linear-least squares.
might not actually be small enough.
You don't know how small is small,
because these are not scalars but operators.
Then the solution may not converge to the minimum you want.
Your solution will depend on where you start from.
I no longer exhibit the nonlinear solver missif
until I find a real data example where it produces noticibly better results
than multistage linear-least squares.
The alternative to linearization is two-stage linear least squares.
In the first stage you estimate the PEF;
in the second you estimate the missing data.
If need be, you can re-estimate the PEF using all the data
both known and missing (downweighted if you prefer).
If you don't have enough regression equations
because your data is irregularly distributed,
then you can use binning.
Still not enough? Try coarser bins.
The point is that nonlinear solvers will not work unless you
begin close enough to the solution,
and the way to get close is by arranging first to
solve a sensible (though approximate) linearized problem.
Only as a last resort, after you have gotten as near as you can,
should you use the nonlinear least-squares techniques.





Next: LEVELED INVERSE INTERPOLATION
Up: BOTH MISSING DATA AND
Previous: Objections to interpolation error
Stanford Exploration Project
4/27/2004
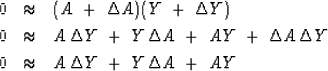
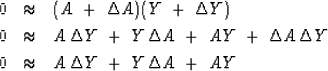
![]() and
and ![]() ).
The free-mask matrix for missing data is denoted
).
The free-mask matrix for missing data is denoted ![]() and that for the PE filter is
and that for the PE filter is ![]() .The fitting goal (39) becomes
.The fitting goal (39) becomes
![\begin{displaymath}
\left[
\begin{array}
{cccccccccc}
a_0& . & . & . & . & . &...
...r r_7 \\ \bar r_8
\end{array} \right]
\quad \approx \ \bold 0\end{displaymath}](img108.gif)
![]() inside the iteration loop
so that as convergence is achieved (if it is achieved),
the neglected nonlinear term
inside the iteration loop
so that as convergence is achieved (if it is achieved),
the neglected nonlinear term ![]() tends to zero.
tends to zero.
![]() might not actually be small enough.
You don't know how small is small,
because these are not scalars but operators.
Then the solution may not converge to the minimum you want.
Your solution will depend on where you start from.
I no longer exhibit the nonlinear solver missif
until I find a real data example where it produces noticibly better results
than multistage linear-least squares.
might not actually be small enough.
You don't know how small is small,
because these are not scalars but operators.
Then the solution may not converge to the minimum you want.
Your solution will depend on where you start from.
I no longer exhibit the nonlinear solver missif
until I find a real data example where it produces noticibly better results
than multistage linear-least squares.