 |
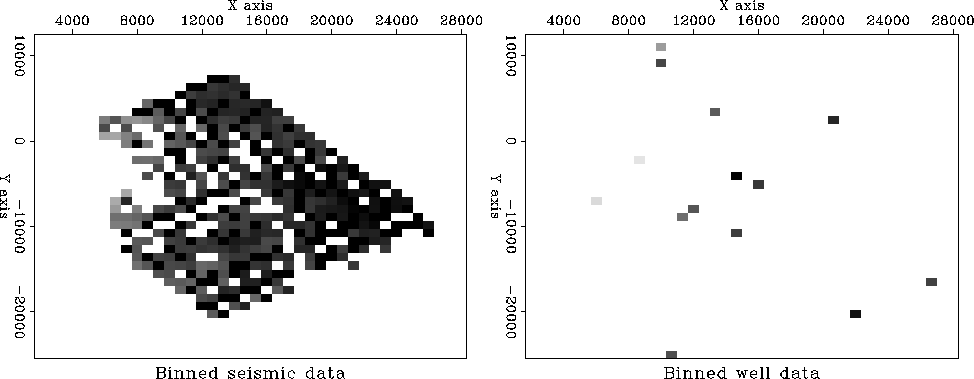
Figure 8 Binning by data push. Left is seismic data. Right is well locations. Values in bins are divided by numbers in bins. (Toldi)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
The binning of the seismic data in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is not really satisfactory when we have available
the techniques of missing data estimation
to fill the empty bins.
Using the ideas of subroutine mis1()
is not really satisfactory when we have available
the techniques of missing data estimation
to fill the empty bins.
Using the ideas of subroutine mis1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
we can extend the seismic data into the empty part of the plane.
We use the same principle that we minimize the energy in
the filtered map where the map must match the data where it is known.
I chose the filter
,
we can extend the seismic data into the empty part of the plane.
We use the same principle that we minimize the energy in
the filtered map where the map must match the data where it is known.
I chose the filter ![]() to be the Laplacian operator (actually, its negative)
to obtain the result in Figure
to be the Laplacian operator (actually, its negative)
to obtain the result in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
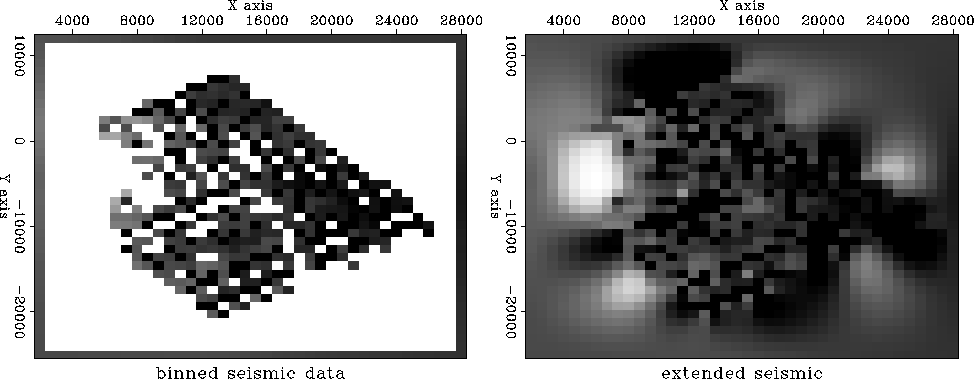 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) also involves a boundary condition calculation.
Many differential equations have a solution that becomes infinite
at infinite distance, and in practice this means that the largest
solutions may often be found on the boundaries of the plot,
exactly where there is the least information.
To obtain a more pleasing result,
I placed artificial ``average'' data
along the outer boundary.
Each boundary point was given the value of an average
of the interior data values.
The average was weighted,
each weight being an inverse power of the separation distance
of the boundary point from the interior point.
also involves a boundary condition calculation.
Many differential equations have a solution that becomes infinite
at infinite distance, and in practice this means that the largest
solutions may often be found on the boundaries of the plot,
exactly where there is the least information.
To obtain a more pleasing result,
I placed artificial ``average'' data
along the outer boundary.
Each boundary point was given the value of an average
of the interior data values.
The average was weighted,
each weight being an inverse power of the separation distance
of the boundary point from the interior point.
Parenthetically, we notice that all the unknown interior points could be guessed by the same method we used on the outer boundary. After some experience guessing what inverse power would be best for the weighting functions, I do not recommend this method. Like gravity, the forces of interpolation from the weighted sums are not blocked by intervening objects. But the temperature in a house is not a function of temperature in its neighbor's house. To further isolate the more remote points, I chose weights to be the inverse fourth power of distance.
The first job is to fill the gaps in the seismic data.
We just finished doing a job like this in one dimension.
I'll give you more computational details later.
Let us call the extended seismic data ![]() .
.
Think of a map of a model space ![]() of infinitely many hypothetical wells that must match the real wells,
where we have real wells.
We must find a map that matches the wells exactly
and somehow matches the seismic information elsewhere.
Let us define the vector
of infinitely many hypothetical wells that must match the real wells,
where we have real wells.
We must find a map that matches the wells exactly
and somehow matches the seismic information elsewhere.
Let us define the vector ![]() as shown in Figure
as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) so
so ![]() is
observed values at wells and zeros elsewhere.
is
observed values at wells and zeros elsewhere.
Where the seismic data contains sharp bumps or streaks,
we want our final earth model to have those features.
The wells cannot provide the rough features because the wells
are too far apart to provide high spatial frequencies.
The well information generally conflicts with the seismic data
at low spatial frequencies because of systematic discrepancies between
the two types of measurements.
Thus we must accept that ![]() and
and ![]() may differ
at low spatial frequencies (where gradient and Laplacian are small).
may differ
at low spatial frequencies (where gradient and Laplacian are small).
Our final map ![]() would be very unconvincing if
it simply jumped from a well value at one point
to a seismic value at a neighboring point.
The map would contain discontinuities around each well.
Our philosophy of finding an earth model
would be very unconvincing if
it simply jumped from a well value at one point
to a seismic value at a neighboring point.
The map would contain discontinuities around each well.
Our philosophy of finding an earth model ![]() is that our earth map should contain no obvious
``footprint'' of the data acquistion (well locations).
We adopt the philosopy that the difference
between the final map (extended wells)
and the seismic information
is that our earth map should contain no obvious
``footprint'' of the data acquistion (well locations).
We adopt the philosopy that the difference
between the final map (extended wells)
and the seismic information ![]() should be smooth.
Thus,
we seek the minimum residual
should be smooth.
Thus,
we seek the minimum residual ![]() which is the roughened difference between the seismic data
which is the roughened difference between the seismic data ![]() and the map
and the map ![]() of hypothetical omnipresent wells.
With roughening operator
of hypothetical omnipresent wells.
With roughening operator ![]() we fit
we fit
| |
(12) |
| (13) |
Now we prepare some roughening operators ![]() .We have already coded a 2-D gradient operator
igrad2
.We have already coded a 2-D gradient operator
igrad2 ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Let us combine it with its adjoint to get the 2-D laplacian operator.
(You might notice that the laplacian operator is ``self-adjoint'' meaning
that the operator does the same calculation that its adjoint does.
Any operator of the form
.
Let us combine it with its adjoint to get the 2-D laplacian operator.
(You might notice that the laplacian operator is ``self-adjoint'' meaning
that the operator does the same calculation that its adjoint does.
Any operator of the form ![]() is self-adjoint because
is self-adjoint because
![]() . )
. )
laplac2Laplacian in 2-D Subroutine lapfill2()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the same idea as mis1()
is the same idea as mis1()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) except that
the filter
except that
the filter ![]() has been specialized to the
laplacian
implemented by module laplac2
has been specialized to the
laplacian
implemented by module laplac2 ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
lapfill2Find 2-D missing data
.
lapfill2Find 2-D missing data
Subroutine lapfill2()
can be used for each of our two problems,
(1) extending the seismic data to fill space, and
(2) fitting the map exactly to the wells and approximately to the seismic data.
When extending the seismic data,
the initially non-zero components ![]() are fixed
and cannot be changed.
That is done by calling
lapfill2() with mfixed=(s/=0.).
When extending wells,
the initially non-zero components
are fixed
and cannot be changed.
That is done by calling
lapfill2() with mfixed=(s/=0.).
When extending wells,
the initially non-zero components ![]() are fixed
and cannot be changed.
That is done by calling
lapfill2() with mfixed=(w/=0.).
are fixed
and cannot be changed.
That is done by calling
lapfill2() with mfixed=(w/=0.).
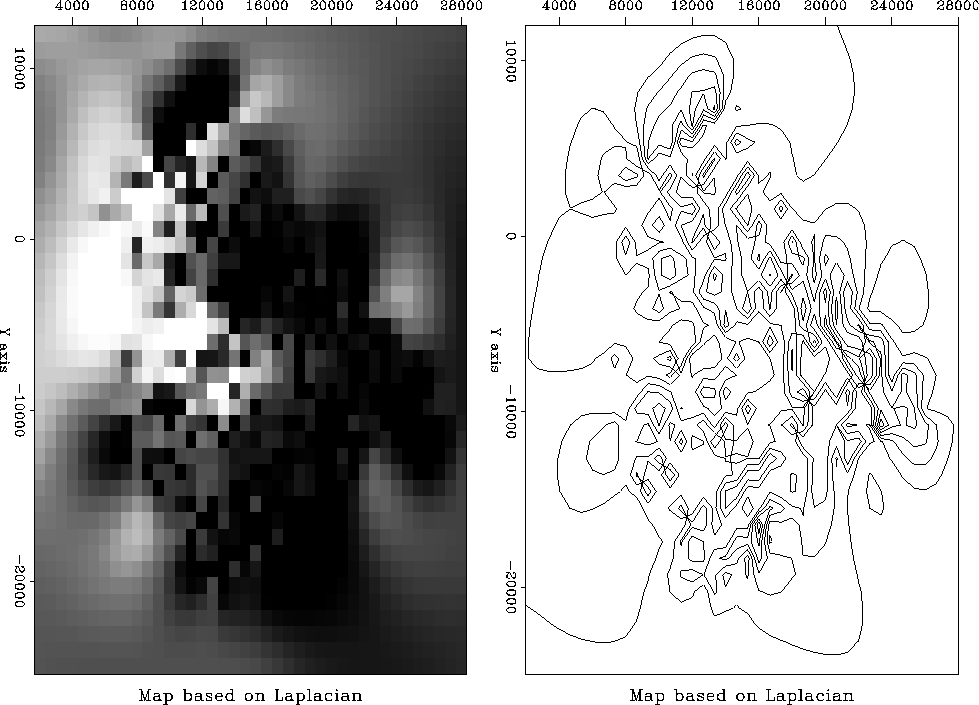
The final map is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
Results can be computed with various filters.
I tried both ![]() and
and ![]() .There are disadvantages of each,
.There are disadvantages of each,
![]() being too cautious and
being too cautious and
![]() perhaps being too aggressive.
Figure
perhaps being too aggressive.
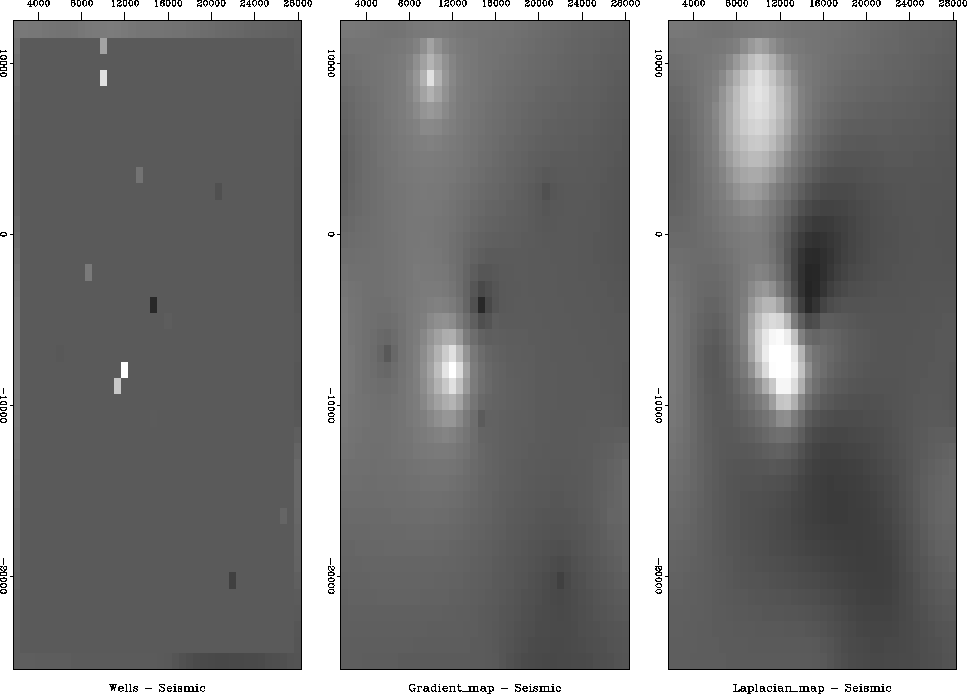
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the difference
shows the difference ![]() between
the extended seismic data and the extended wells.
Notice that for
between
the extended seismic data and the extended wells.
Notice that for ![]() the difference shows
a localized ``tent pole'' disturbance about each well.
For
the difference shows
a localized ``tent pole'' disturbance about each well.
For ![]() there could be large overshoot between wells,
especially if two nearby wells have significantly different values.
I don't see that problem here.
there could be large overshoot between wells,
especially if two nearby wells have significantly different values.
I don't see that problem here.
My overall opinion is that the Laplacian does the better job in this case. I have that opinion because in viewing the extended gradient I can clearly see where the wells are. The wells are where we have acquired data. We'd like our map of the world to not show where we acquired data. Perhaps our estimated map of the world cannot help but show where we have and have not acquired data, but we'd like to minimize that aspect.
| A good image of the earth hides our data acquisition footprint. |
 |
To understand the behavior theoretically,
recall that in one dimension
the filter ![]() interpolates with straight lines
and
interpolates with straight lines
and ![]() interpolates with cubics.
This is because the fitting goal
interpolates with cubics.
This is because the fitting goal
![]() ,leads to
,leads to
![]() or
or ![]() , whereas the fitting goal
, whereas the fitting goal
![]() leads to
leads to
![]() which is satisfied by cubics.
In two dimensions, minimizing the output of
which is satisfied by cubics.
In two dimensions, minimizing the output of ![]() gives us solutions of Laplace's equation with sources at the known data.
It is as if
gives us solutions of Laplace's equation with sources at the known data.
It is as if ![]() stretches a rubber sheet over poles at each well,
whereas
stretches a rubber sheet over poles at each well,
whereas ![]() bends a stiff plate.
bends a stiff plate.
Just because ![]() gives smoother maps than
gives smoother maps than ![]() does not mean those maps are closer to reality.
This is a deeper topic, addressed in Chapter
does not mean those maps are closer to reality.
This is a deeper topic, addressed in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
It is the same issue we noticed when comparing
figures
.
It is the same issue we noticed when comparing
figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.