Next: Nearest-neighbor normal moveout (NMO)
Up: FAMILIAR OPERATORS
Previous: Backsolving, polynomial division and
Many geophysical measurements contain
very low-frequency noise called ``drift.''
For example, it might take some months to survey the depth of a lake.
Meanwhile, rainfall or evaporation could change the lake level so that
new survey lines become inconsistent with old ones.
Likewise, gravimeters are sensitive to atmospheric pressure,
which changes with the weather.
A magnetic survey of an archeological site would need to contend
with the fact that the earth's main magnetic field is changing randomly
through time while the survey is being done.
Such noises are sometimes called ``secular noise.''
The simplest way to eliminate low frequency noise is
to take a time derivative.
A disadvantage is that the derivative
changes the waveform
from a pulse to a doublet (finite difference).
Here we examine the most basic low-cut filter.
It preserves the waveform at high frequencies;
it has an adjustable parameter
for choosing the bandwidth of the low cut;
and it is causal (uses the past but not the future).
We make our causal lowcut filter (highpass filter) by
two stages which can be done in either order.
- 1.
- Apply a time derivative, actually a finite
difference, convolving the data with (1,-1).
- 2.
- Integrate, actually to do a leaky integration,
to deconvolve with
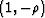 where numerically,
where numerically,
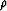 is slightly less than unity.
is slightly less than unity.
The convolution ensures that the zero frequency is removed.
The leaky integration almost undoes the differentiation
(but does not restore the zero frequency).
Adjusting the numerical value of  adjusts
the cutoff frequency of the filter.
To learn the impulse response of the combined processes, we
need to convolve the finite difference (1,-1)
with the leaky integration
adjusts
the cutoff frequency of the filter.
To learn the impulse response of the combined processes, we
need to convolve the finite difference (1,-1)
with the leaky integration
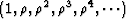 .The result is
.The result is
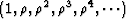 minus
minus
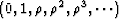 .We can think of this as
.We can think of this as
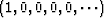 minus
minus
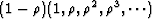 .In other words the impulse response is an impulse
followed by the negative of a weak
.In other words the impulse response is an impulse
followed by the negative of a weak 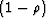 decaying exponential
decaying exponential 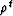 .Roughly speaking, the cutoff frequency of the filter corresponds
to matching one wavelength to the exponential decay time.
.Roughly speaking, the cutoff frequency of the filter corresponds
to matching one wavelength to the exponential decay time.
Some exercise with Fourier transforms
or Z-transforms![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ,
shows the
Fourier transform of this highpass filter filter
to be
,
shows the
Fourier transform of this highpass filter filter
to be
| ![\begin{displaymath}
H(Z) \eq {1-Z \over 1-\rho Z}
\eq
1
-(1-\rho) [
Z^1
+\rho Z^2
+\rho^2 Z^3
+\rho^3 Z^4
\cdots
]\end{displaymath}](img88.gif) |
(25) |
where the unit-delay operator is 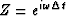 and where
and where 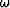 is the frequency.
A symmetical (noncausal) lowcut filter would filter once forward
with H(Z) and once backwards (adjoint) with H(1/Z).
This is not the place for a detailed Fourier analysis of this filter
but it is the place to mention that a cutoff filter is typically
specified by its cutoff frequency,
a frequency that separates the pass and reject region.
For this filter, the cutoff frequency
is the frequency.
A symmetical (noncausal) lowcut filter would filter once forward
with H(Z) and once backwards (adjoint) with H(1/Z).
This is not the place for a detailed Fourier analysis of this filter
but it is the place to mention that a cutoff filter is typically
specified by its cutoff frequency,
a frequency that separates the pass and reject region.
For this filter, the cutoff frequency 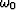 would correspond to matching a quarter wavelength of a sinusoid
to the exponential decay length of
would correspond to matching a quarter wavelength of a sinusoid
to the exponential decay length of 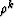 , namely,
say the value of k for which
, namely,
say the value of k for which 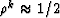
Seismological data is more complex. A single ``measurement''
consists of an explosion and echo signals recorded at many locations.
As before, a complete survey is a track (or tracks)
of explosion locations.
Thus, in seismology, data space is higher dimensional.
Its most troublesome noise is not simply low frequency;
it is low velocity.
We will do more with multidimensional data in later chapters.

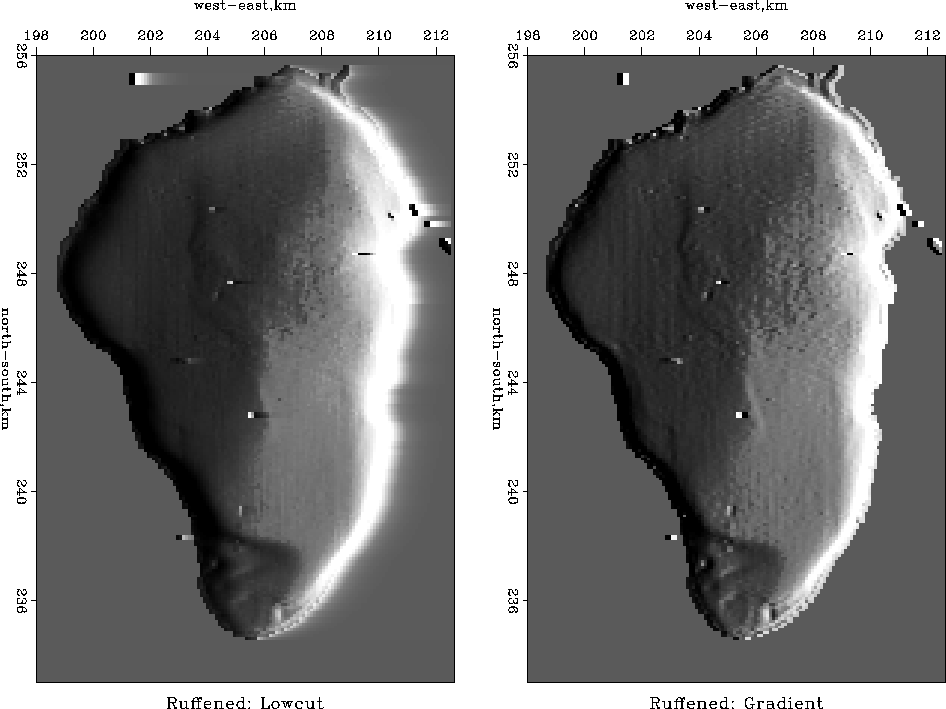
galocut90
Figure 6
The depth of the Sea of Galilee after roughening.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Nearest-neighbor normal moveout (NMO)
Up: FAMILIAR OPERATORS
Previous: Backsolving, polynomial division and
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ,
shows the
Fourier transform of this highpass filter filter
to be
,
shows the
Fourier transform of this highpass filter filter
to be