




Next: Velocity increasing linearly with
Up: CURVED WAVEFRONTS
Previous: Nonhyperbolic curves
We could work out the mathematical problem
of finding an analytic solution for
the travel time
as a function of distance in an earth with stratified v(z),
but the more difficult problem is
the practical one which is the reverse,
finding 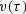 from the travel time curves.
Mathematically we can
express the travel time (squared)
as a power series in distance h.
Since everything is symmetric in h,
we have only even powers.
The practitioner's approach is to look at small offsets
and thus ignore h4 and higher powers.
Velocity then enters only as the coefficient of h2.
Let us why it is the RMS velocity,
equation (25),
that enters this coefficient.
from the travel time curves.
Mathematically we can
express the travel time (squared)
as a power series in distance h.
Since everything is symmetric in h,
we have only even powers.
The practitioner's approach is to look at small offsets
and thus ignore h4 and higher powers.
Velocity then enters only as the coefficient of h2.
Let us why it is the RMS velocity,
equation (25),
that enters this coefficient.
The hyperbolic form of equation (24) will generally not be exact
when h is very large.
For ``sufficiently'' small h,
the derivation of the hyperbolic shape follows
from application of Snell's law at each interface.
Snell's law implies that the Snell parameter p, defined by
| 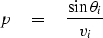 |
(36) |
is a constant along both raypaths in Figure 10.
Inspection of Figure 10 shows that
in the ith layer
the raypath horizontal distance 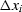 and travel time
and travel time 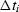 are given on the left below by
are given on the left below by
| 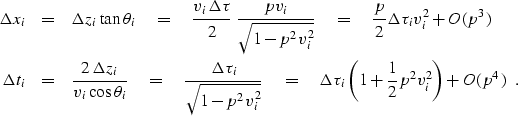 |
(37) |
| (38) |
The center terms above arise by using equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
to represent
)
to represent 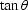 and
and 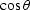 as a function of
as a function of 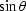 hence p,
and the right sides above come from expanding in powers of p.
Any terms of order p3 or higher will be discarded,
since these become important only at large values of h.
Summing equation (
hence p,
and the right sides above come from expanding in powers of p.
Any terms of order p3 or higher will be discarded,
since these become important only at large values of h.
Summing equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) over all layers
yields the half-offset h separating the midpoint
from the geophone location and the total travel time t.
) over all layers
yields the half-offset h separating the midpoint
from the geophone location and the total travel time t.
| 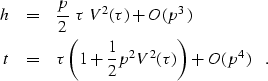 |
(39) |
| (40) |
Solving equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for p gives
) for p gives 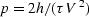 ,justifying the neglect of the O(p3) terms when h is small.
Substituting this value of p into equation (
,justifying the neglect of the O(p3) terms when h is small.
Substituting this value of p into equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields
) yields
| 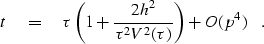 |
(41) |
Squaring both sides and discarding terms of order h4 and p4
yields the advertised result, equation (24).
XXXXXXXX





Next: Velocity increasing linearly with
Up: CURVED WAVEFRONTS
Previous: Nonhyperbolic curves
Stanford Exploration Project
12/26/2000
![]() from the travel time curves.
Mathematically we can
express the travel time (squared)
as a power series in distance h.
Since everything is symmetric in h,
we have only even powers.
The practitioner's approach is to look at small offsets
and thus ignore h4 and higher powers.
Velocity then enters only as the coefficient of h2.
Let us why it is the RMS velocity,
equation (25),
that enters this coefficient.
from the travel time curves.
Mathematically we can
express the travel time (squared)
as a power series in distance h.
Since everything is symmetric in h,
we have only even powers.
The practitioner's approach is to look at small offsets
and thus ignore h4 and higher powers.
Velocity then enters only as the coefficient of h2.
Let us why it is the RMS velocity,
equation (25),
that enters this coefficient.
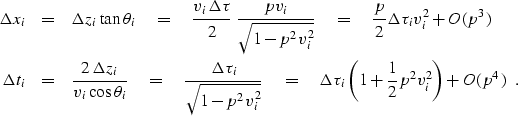
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
to represent
)
to represent ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) over all layers
yields the half-offset h separating the midpoint
from the geophone location and the total travel time t.
) over all layers
yields the half-offset h separating the midpoint
from the geophone location and the total travel time t.
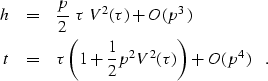
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for p gives
) for p gives ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields
) yields