




Next: Layered media
Up: CURVED WAVEFRONTS
Previous: CURVED WAVEFRONTS
When a ray travels in a depth-stratified medium,
Snell's parameter 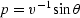 is constant along the ray.
If the ray emerges at the surface,
we can measure the distance x that it has traveled,
the time t it took, and its apparent speed dx/dt=1/p.
A well-known estimate
is constant along the ray.
If the ray emerges at the surface,
we can measure the distance x that it has traveled,
the time t it took, and its apparent speed dx/dt=1/p.
A well-known estimate 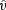 for the earth velocity contains this apparent speed.
for the earth velocity contains this apparent speed.
| 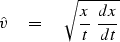 |
(18) |
To see where this velocity estimate comes from,
first notice that the stratified velocity v(z) can be parameterized
as a function of time and take-off angle of a ray from the surface.
| 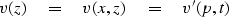 |
(19) |
The x coordinate of the tip of a ray with Snell parameter p is
the horizontal component of velocity integrated over time.
| 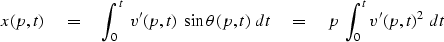 |
(20) |
Inserting this into equation (18)
and canceling p=dt/dx we have
| 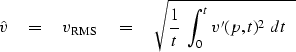 |
(21) |
which shows that the observed velocity is the ``root-mean-square'' velocity.
When velocity varies with depth,
the traveltime curve is only roughly a hyperbola.
If we break the event into many short line segments where the
i-th segment has a slope pi and a midpoint (ti,xi)
each segment gives a different 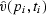 and we have the unwelcome chore of assembling the best model.
Instead, we can fit the observational data to the best fitting hyperbola
using a different velocity hyperbola for each apex,
in other words,
find
and we have the unwelcome chore of assembling the best model.
Instead, we can fit the observational data to the best fitting hyperbola
using a different velocity hyperbola for each apex,
in other words,
find 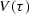 so this equation
will best flatten the data in
so this equation
will best flatten the data in 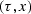 -space.
-space.
| 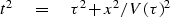 |
(22) |
Differentiate with respect to x at constant  getting
getting
| 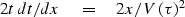 |
(23) |
which confirms that the observed velocity
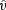 in equation (18),
is the same as
in equation (18),
is the same as 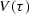 no matter where you measure
no matter where you measure
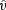 on a hyperbola.
on a hyperbola.





Next: Layered media
Up: CURVED WAVEFRONTS
Previous: CURVED WAVEFRONTS
Stanford Exploration Project
12/26/2000
![]() is constant along the ray.
If the ray emerges at the surface,
we can measure the distance x that it has traveled,
the time t it took, and its apparent speed dx/dt=1/p.
A well-known estimate
is constant along the ray.
If the ray emerges at the surface,
we can measure the distance x that it has traveled,
the time t it took, and its apparent speed dx/dt=1/p.
A well-known estimate ![]() for the earth velocity contains this apparent speed.
for the earth velocity contains this apparent speed.
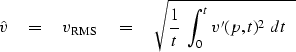
![]() and we have the unwelcome chore of assembling the best model.
Instead, we can fit the observational data to the best fitting hyperbola
using a different velocity hyperbola for each apex,
in other words,
find
and we have the unwelcome chore of assembling the best model.
Instead, we can fit the observational data to the best fitting hyperbola
using a different velocity hyperbola for each apex,
in other words,
find ![]() so this equation
will best flatten the data in
so this equation
will best flatten the data in ![]() -space.
-space.