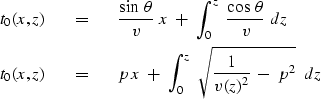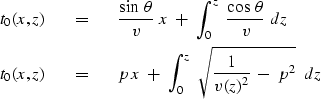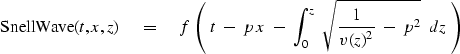Next: CURVED WAVEFRONTS
Up: DIPPING WAVES
Previous: Evanescent waves
The above differential equations will often reoccur in later analysis,
so they are very important.
Interestingly, these differential equations have a simple solution.
Taking the Snell wave to go through the origin at time zero,
an expression for the
arrival time of the Snell wave at any other location
is given by
| 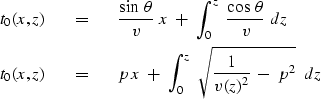 |
(12) |
| (13) |
The validity of equations (12) and (13)
is readily checked by
computing 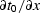 and
and 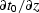 ,then comparing with (10) and (11).
,then comparing with (10) and (11).
An arbitrary waveform f(t) may be carried by the Snell wave.
Use (12) and (13) to define the time t0 for
a delayed wave f[t-t0 (x,z)] at the location (x,z).
| 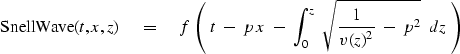 |
(14) |
Equation (14)
carries an arbitrary signal throughout the whole medium.
Interestingly, it does not agree with wave propagation theory
or real life because
equation (14) does not correctly account for amplitude
changes that result from
velocity changes and reflections.
Thus it is said that
Equation (14)
is ``kinematically'' correct but ``dynamically'' incorrect.
It happens that most industrial data processing only requires
things to be kinematically correct,
so this expression is a usable one.





Next: CURVED WAVEFRONTS
Up: DIPPING WAVES
Previous: Evanescent waves
Stanford Exploration Project
12/26/2000