An important transformation in exploration geophysics takes data as a function of shot-receiver offset and transforms it to data as a function of apparent velocity. Data is summed along hyperbolas of many velocities. This important industrial process is adjoint to another that may be easier to grasp: data is synthesized by a superposition of many hyperbolas. The hyperbolas have various asymptotes (velocities) and various tops (apexes). Pseudocode for these transformations is
do v {
do  {
do x {
{
do x {
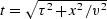 if hyperbola superposition
data(t,x) = data(t,x) + vspace
if hyperbola superposition
data(t,x) = data(t,x) + vspace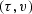 else if velocity analysis
vspace
else if velocity analysis
vspace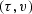 = vspace
= vspace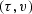 + data(t,x)
}}}
+ data(t,x)
}}}
We can ask the question, if we transform data to velocity space,
and then return to data space,
will we get the original data?
Likewise we could begin from the velocity space,
synthesize some data, and return to velocity space.
Would we come back to where we started?
The answer is yes, in some degree.
Mathematically, the question amounts to this:
Given the operator ![]() , is
, is ![]() approximately
an identity operator, i.e. is
approximately
an identity operator, i.e. is ![]() nearly a unitary operator?
It happens that
nearly a unitary operator?
It happens that ![]() defined by the pseudocode above
is rather far from an identity transformation,
but we can bring it much closer
by including some simple scaling factors.
It would be a lengthy digression here to derive all these weighting factors
but let us briefly see the motivation for them.
One weight arises because waves lose amplitude as they spread out.
Another weight arises because some angle-dependent effects should be taken
into account. A third weight arises because in creating a velocity space,
the near offsets are less important than the wide offsets
and we do not even need the zero-offset data.
A fourth weight is a frequency dependent one
which is explained in chapter
defined by the pseudocode above
is rather far from an identity transformation,
but we can bring it much closer
by including some simple scaling factors.
It would be a lengthy digression here to derive all these weighting factors
but let us briefly see the motivation for them.
One weight arises because waves lose amplitude as they spread out.
Another weight arises because some angle-dependent effects should be taken
into account. A third weight arises because in creating a velocity space,
the near offsets are less important than the wide offsets
and we do not even need the zero-offset data.
A fourth weight is a frequency dependent one
which is explained in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Basically, the summations in the velocity transformation are like integrations,
thus they tend to boost low frequencies.
This could be compensated by scaling
in the frequency domain
with frequency as
.
Basically, the summations in the velocity transformation are like integrations,
thus they tend to boost low frequencies.
This could be compensated by scaling
in the frequency domain
with frequency as ![]() with subroutine halfdifa()
with subroutine halfdifa() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The weighting issue will be examined in more detail later.
Meanwhile, we can see nice quality examples
from very simple programs
if we include the weights
in the physical domain, ![]() .(Typographical note: Do not confuse
the weight w (double you) with omega
.(Typographical note: Do not confuse
the weight w (double you) with omega ![]() .)
To avoid the coding clutter of the frequency domain weighting
.)
To avoid the coding clutter of the frequency domain weighting
![]() I omit that,
thus getting smoother results than theoretically preferable.
Figure 8 illustrates this smoothing by starting
from points in velocity space, transforming to offset,
and then back and forth again.
I omit that,
thus getting smoother results than theoretically preferable.
Figure 8 illustrates this smoothing by starting
from points in velocity space, transforming to offset,
and then back and forth again.
 |
There is one final complication relating to weighting.
The most symmetrical approach is to put
w into both ![]() and
and ![]() .This is what subroutine velsimp()
.This is what subroutine velsimp() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) does.
Thus, because of the weighting by
does.
Thus, because of the weighting by ![]() ,the synthetic data in Figure 8 is
nonphysical.
An alternate view is to define
,the synthetic data in Figure 8 is
nonphysical.
An alternate view is to define ![]() (by the pseudo code above, or by some modeling theory)
and then for reverse transformation
use
(by the pseudo code above, or by some modeling theory)
and then for reverse transformation
use ![]() .
.
# velsimp -- simple velocity transform
#
subroutine velsimp( adj,add, t0,dt,x0,dx,s0,ds, nt,nx,ns, modl, data)
integer it,ix,is, adj,add, nt,nx,ns, iz,nz
real x,s,sx, t,z, z0,dz,wt, t0,dt,x0,dx,s0,ds, modl(nt,ns),data(nt,nx)
call adjnull( adj,add, modl,nt*ns, data,nt*nx)
nz= nt; z0=t0; dz= dt; # z is travel time depth
do is= 1, ns { s = s0 + (is-1) * ds
do ix= 1, nx { x = x0 + (ix-1) * dx
do iz= 2, nz { z = z0 + (iz-1) * dz
sx = abs( s * x)
t = sqrt( z * z + sx * sx)
it = 1.5 + (t - t0) / dt
if ( it <= nt) { wt= (z/t) / sqrt( t)
if( adj == 0 )
data(it,ix) = data(it,ix) + modl(iz,is) * sx * wt
else
modl(iz,is) = modl(iz,is) + data(it,ix) * sx * wt
}
}}}
return; end
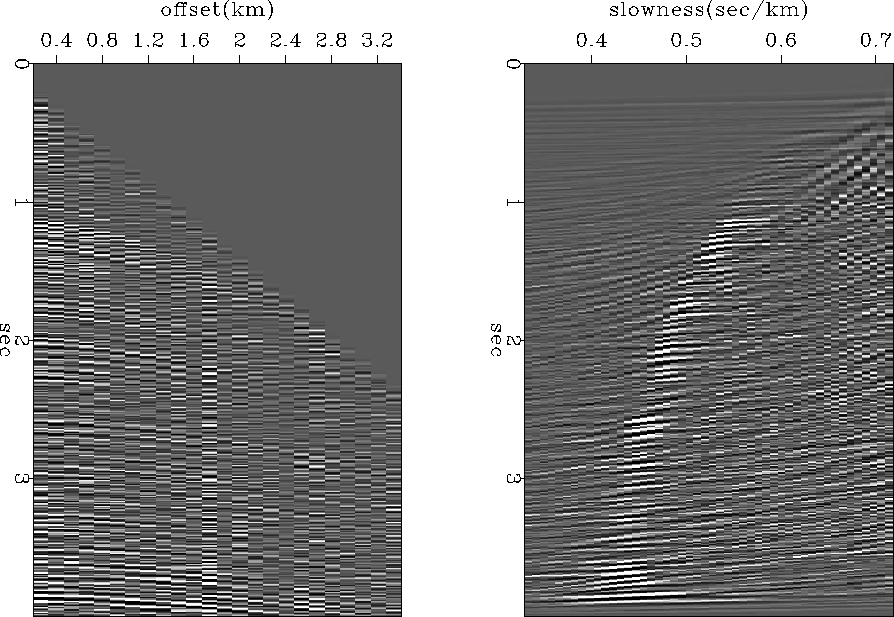
An example of applying subroutine velsimp() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to field data is shown in Figure 9.
to field data is shown in Figure 9.
 |