




Next: MIGRATION WITH ANTIALIASING
Up: MIMICING FIELD ARRAY ANTIALIASING
Previous: NMO and stack with
We should take some care with anti-aliasing in data processing.
The anti-aliasing measures we take, however,
need not match the field recording.
If the field arrays were rectangles,
we could use triangles or sincs in the data processing.
It happens that triangles are an easy extension
of the rectangle work that we have been doing
and triangles make a big step in the right direction.
For an input pulse,
the output of integration is a step.
The output of a second integration is a ramp.
For an input triplet (1, 0, 0, -2, 0, 0, 1)
the output of two integrations is a short triangle.
An easy way to assure time alignment
of the triangle center with
the triplet center is to integrate
once causally and once anticausally
as done in subroutine doubint() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
# Double integration, first causal, then anticausal.
#
subroutine doubint( adj, add, n, pp , qq )
integer adj, add, n; real pp(n), qq(n)
temporary real tt(n)
call adjnull( adj, add, pp,n, qq,n)
if( adj == 0 ) { call causint( 0, 0, n,pp, tt )
call causint( 1, add, n,qq, tt )
}
else { call causint( 1, 0, n,tt, qq )
call causint( 0, add, n,tt, pp )
}
return; end
You can imagine placing the ends and apex of each triangle
at a nearest neighbor mesh point as we did with the rectangles.
Instead I place these ends more precisely on the mesh with
linear interpolation.
Subroutine lint1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) does linear interpolation,
but here we need weighted results
as provided by spotw()
does linear interpolation,
but here we need weighted results
as provided by spotw() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
# Scaled linear interpolation.
#
subroutine spotw( adj, add, scale, nt,t0,dt, t, val, vec )
integer it,itc, adj, add, nt
real tc, fraction, scale, t0,dt, t, val, vec(nt)
call adjnull( adj, add, val,1, vec,nt)
tc = .5+ (t-t0) / dt; itc = tc; it = 1 + itc; fraction = tc - itc
if( 1 <= it && it < nt) {
if( adj == 0) {
vec(it ) = vec(it ) + (1.-fraction) * val * scale
vec(it+1) = vec(it+1) + fraction * val * scale
}
else
val = val + ((1.-fraction) * vec(it) +
fraction * vec(it+1) ) * scale
}
else
call erexit('spotw: at boundary')
return; end
Using these subroutines,
I assembled the stacking subroutine tristack()
and the NMO routine trimo() with triangle wavelets.
The triangle routines are like those for rectangles
except for some minor changes.
Instead of computing the theoretical locations
of impulses on nearer and further traces,
I assumed a straight line tangent to the hyperbola
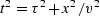 .Differentiating by x at constant
.Differentiating by x at constant  gives the slope
dt/dx= x/(v2t).
As before, the area of the the wavelets, now triangles must be preserved.
The area of a triangle is proportional to the base times the height.
Since the triangles are built from double integration ramp functions,
the height is proportional to the base length.
Thus to preserve areas, each wavelet is scaled by the inverse squared
of the triangle's base length.
Results are shown in
Figures 7 and 8.
gives the slope
dt/dx= x/(v2t).
As before, the area of the the wavelets, now triangles must be preserved.
The area of a triangle is proportional to the base times the height.
Since the triangles are built from double integration ramp functions,
the height is proportional to the base length.
Thus to preserve areas, each wavelet is scaled by the inverse squared
of the triangle's base length.
Results are shown in
Figures 7 and 8.
trimo0
Figure 7
Triangle wavelets,
accurately positioned,
but aliased
(antialias=0.)
|
|  |





trimo1
Figure 8
Antialiased triangle wavelets.
(antialias=1.)
Where ever triangle duration is more than about three points,
the end of one triangle marks the apex of the next.
|
|  |





# Modeling and stacking using triangle weighted moveout.
#
subroutine tristack( adj,add, slow,anti,t0,dt,x0,dx, nt,nx, stack, gather )
integer ix, adj,add, nt,nx
real x, slow(nt),anti,t0,dt,x0,dx, stack(nt), gather(nt,nx)
call adjnull( adj, add, stack,nt, gather,nt*nx)
do ix= 1, nx { x = x0 + dx * (ix-1)
call trimo( adj,1,t0,dt,dx, x, nt,slow,0.,1.,anti,stack, gather(1,ix))
}
return; end
# moveout with triangle shaped smoothing window.
#
subroutine trimo( adj, add, t0,dt, dx,x, nt, slow, s02, wt, anti, zz, tt )
integer iz,itp,itm,adj, add, nt
real t0,dt, dx,x, slow(nt), s02, wt, anti, zz(nt),tt(nt)
real z, t,tm,tp, amp, slope
temporary real ss(nt)
call null( ss,nt); call adjnull( adj, add, zz,nt, tt,nt)
if( adj != 0 ) call doubint( 1, 0, nt, ss, tt)
do iz= 2, nt { z = t0 + dt * (iz-1)
t = sqrt( z**2 + (slow(iz) * x)**2 )
slope = anti * ( slow(iz)**2 - s02 ) * x / t
tp = t + abs(slope * dx) + dt; itp = 1.5 + (tp-t0) / dt
tm = t - abs(slope * dx) - dt; itm = 1.5 + (tm-t0) / dt
if( itm <= 1 ) next
if( itp >= nt ) break
amp = wt * sqrt( nt*dt/t) * z/t * (dt/(dt+tp-tm)) ** 2
call spotw( adj, 1, -amp, nt,t0,dt,tm, zz(iz), ss)
call spotw( adj, 1, 2*amp, nt,t0,dt,t , zz(iz), ss)
call spotw( adj, 1, -amp, nt,t0,dt,tp, zz(iz), ss)
}
if( adj == 0) call doubint( 0, add, nt, ss, tt)
return; end
From the stack reconstruction of the model in Figure 8
we see the reconstruction is more blured with antialiasing
than it was without in Figure 7.
The benefit of antialiasing will become clear next
in more complicated examples where events cross.





Next: MIGRATION WITH ANTIALIASING
Up: MIMICING FIELD ARRAY ANTIALIASING
Previous: NMO and stack with
Stanford Exploration Project
12/26/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

