




Next: Kirchhoff artifacts
Up: HYPERBOLA PROGRAMMING
Previous: Tutorial Kirchhoff code
Subroutine kirchslow() can easily be speeded by a factor
that is commonly more than 30.
The philosopy of this book is to avoid minor optimizations,
but a factor of 30 really is significant,
and the analysis required for the speed up is also interesting.
Much of the inefficiency of kirchslow() arises when
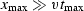 because then many values of t
are computed beyond
because then many values of t
are computed beyond 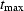 .To avoid this,
we notice that for fixed offset (ix-iy) and variable depth iz,
as depth increases,
time it eventually goes beyond the bottom of the mesh
and, as soon as this happens,
it will continue to happen for all larger values of iz.
Thus we can break out of the iz loop the first time
we go off the mesh to avoid computing anything beyond
as shown in subroutine kirchfast().
(Some quality compromises, limiting the aperature or the dip,
also yield speedup, but we avoid those.)
Another big speedup arises from reusing square roots.
Since the square root depends only on offset and depth,
once computed it can be used for all ix.
Finally, these changes of variables have left us
with more complicated side boundaries,
but once we work these out,
the inner loops can be devoid of tests and
in kirchfast()
they are in a form that is highly optimizable by many compilers.
.To avoid this,
we notice that for fixed offset (ix-iy) and variable depth iz,
as depth increases,
time it eventually goes beyond the bottom of the mesh
and, as soon as this happens,
it will continue to happen for all larger values of iz.
Thus we can break out of the iz loop the first time
we go off the mesh to avoid computing anything beyond
as shown in subroutine kirchfast().
(Some quality compromises, limiting the aperature or the dip,
also yield speedup, but we avoid those.)
Another big speedup arises from reusing square roots.
Since the square root depends only on offset and depth,
once computed it can be used for all ix.
Finally, these changes of variables have left us
with more complicated side boundaries,
but once we work these out,
the inner loops can be devoid of tests and
in kirchfast()
they are in a form that is highly optimizable by many compilers.
# Kirchhoff migration and diffraction. (greased lightning)
#
subroutine kirchfast( adj, add, vrms, t0,dt,dx, modl,nt,nx, data)
integer ix,iz,it,ib, adj, add, nt,nx
real amp,t,z,b, vrms(nt), t0,dt,dx, modl(nt,nx),data(nt,nx)
call adjnull( adj, add, modl,nt*nx, data,nt*nx)
do ib= -nx, nx { b = dx * ib # b = offset
do iz= 2, nt { z = t0 + dt * (iz-1) # z = travel-time depth
t = sqrt( z**2 + (b*2/vrms(iz))**2 )
it = 1.5 + (t - t0) / dt
if( it > nt ) break
amp = (z / t) * sqrt( nt*dt / t )
do ix= max0(1, 1-ib), min0(nx, nx-ib)
if( adj == 0 )
data(it,ix+ib)=data(it,ix+ib)+modl(iz,ix )*amp
else
modl(iz,ix )=modl(iz,ix )+data(it,ix+ib)*amp
}
}
return; end
Originally the two Kirchhoff programs produced identical output,
but finally I could not resist adding an important feature
to the fast program,
scale factors 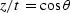 and
and 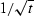 that are described elsewhere.
The fast program
allows for velocity variation with depth.
When velocity varies laterally the story becomes much more complicated.
that are described elsewhere.
The fast program
allows for velocity variation with depth.
When velocity varies laterally the story becomes much more complicated.
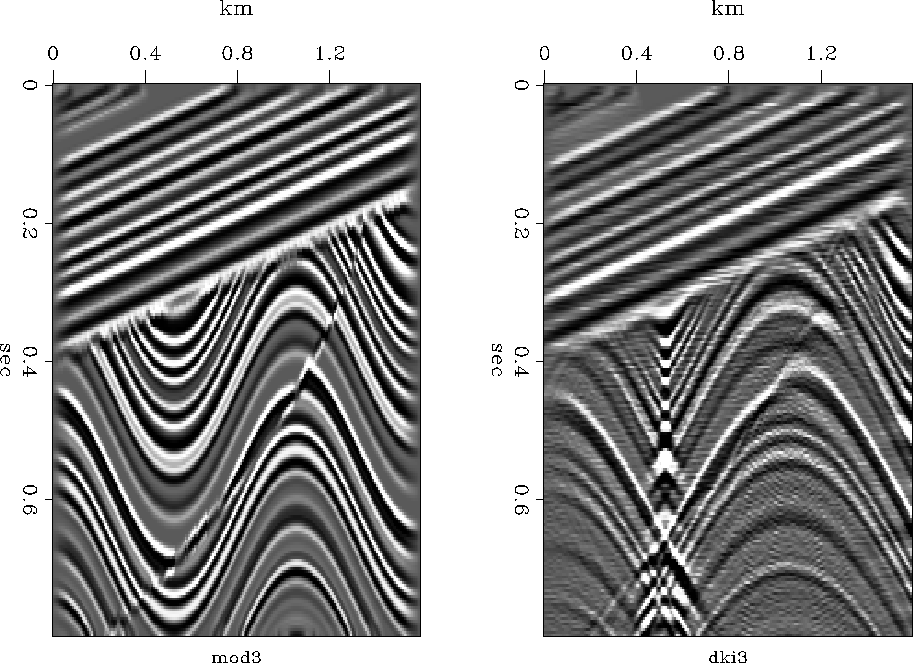
Figure 6 shows an example.
The model includes dipping beds, syncline, anticline, fault,
unconformity, and buried focus.
The result is as expected with a ``bow tie'' at the buried focus.
On a video screen, I can see hyperbolic events originating
from the unconformity and the fault.
At the right edge are a few faint edge artifacts.
We could have reduced or eliminated these edge artifacts
if we had extended the model to the sides with some empty space.
kfgood
Figure 6
Left is the model.
Right is diffraction to synthetic data.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Kirchhoff artifacts
Up: HYPERBOLA PROGRAMMING
Previous: Tutorial Kirchhoff code
Stanford Exploration Project
12/26/2000
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)