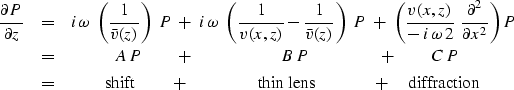
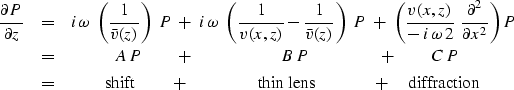 |
(9) | |
| (10) |
Mathematicians look at the problem this way:
Consider any fixed wave propagation angle
so ![]() is a constant.
Now let frequency
is a constant.
Now let frequency ![]() (and hence kx) tend together to infinity.
The terms in BCP and CBP grow in proportion to the second power
of frequency,
whereas those in (BC-CB)P grow as lower powers.
There is however, a catch.
The material properties have a ``wavelength'' too.
We can think of (dv/dx)/v as a spatial wavenumber
for the material just as kx is a spatial wavenumber for the wave.
If the material contains a step function change in its properties,
that is an infinite spatial frequency (dv/dx)/v for the material.
Then the (BC-CB)P terms dominate near the place where
one material changes to another.
If we drop the (BC-CB)P terms,
we'll get the transmission coefficient incorrect,
although everything would be quite fine everywhere else
except at the boundary.
(and hence kx) tend together to infinity.
The terms in BCP and CBP grow in proportion to the second power
of frequency,
whereas those in (BC-CB)P grow as lower powers.
There is however, a catch.
The material properties have a ``wavelength'' too.
We can think of (dv/dx)/v as a spatial wavenumber
for the material just as kx is a spatial wavenumber for the wave.
If the material contains a step function change in its properties,
that is an infinite spatial frequency (dv/dx)/v for the material.
Then the (BC-CB)P terms dominate near the place where
one material changes to another.
If we drop the (BC-CB)P terms,
we'll get the transmission coefficient incorrect,
although everything would be quite fine everywhere else
except at the boundary.
A question is, to what degree do the terms commute? The problem is just that of focusing a slide projector. Adjusting the focus knob amounts to repositioning the thin-lens term in comparison to the free-space diffraction term. There is a small range of knob positions over which no one can notice any difference, and a larger range over which the people in the back row are not disturbed by misfocus. Much geophysical data processing amounts to downward extrapolation of data. The lateral velocity variation
occurring in the lens term is known only to a limited accuracy and we often wish to determine v(x) by the extrapolation procedure.
In practice it seems best to forget the (BC-CB)P terms because we hardly ever know the material properties very well anyway. Then we split, doing the shift and the thin-lens part analytically while doing the diffraction part by a numerical method.