|
dcretard
Figure 4 Left shows a superposition of the hyperbolas of Figure 3. At the right the superposition incorporates a shift, called retardation | 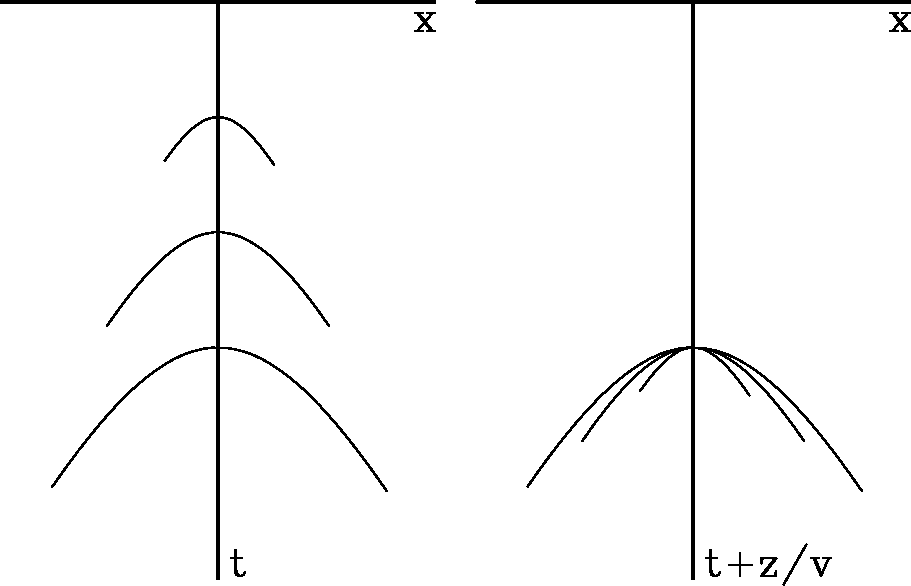 |
A dictionary gives many definitions for the word run. They are related, but they are distinct. Similarly, the word migration in geophysical prospecting has about four related but distinct meanings. The simplest is like the meaning of the word move. When an object at some location in the (x , z)-plane is found at a different location at a later time t, then we say it moves. Analogously, when a wave arrival (often called an event ) at some location in the (x , t)-space of geophysical observations is found at a different position for a different survey line at a greater depth z, then we say it migrates.
To see this more clearly, imagine the four frames of Figure 3 being taken from a movie. During the movie, the depth z changes beginning at the beach (the earth's surface) and going out to the storm barrier. The frames are superimposed in Figure 4(left).
|
dcretard
Figure 4 Left shows a superposition of the hyperbolas of Figure 3. At the right the superposition incorporates a shift, called retardation |  |
Mainly what happens in the movie is that the event migrates upward toward t=0. To remove this dominating effect of vertical translation we make another superposition, keeping the hyperbola tops all in the same place. Mathematically, the time t axis is replaced by a so-called retarded time axis t ' = t + z/v, shown in Figure 4(right). The second, more precise definition of migration is the motion of an event in ( x , t ' )-space as z changes. After removing the vertical shift, the residual motion is mainly a shape change. By this definition, hyperbola tops, or horizontal layers, do not migrate.
The hyperbolas in Figure 4 really extend to infinity,
but the drawing cuts each one off at a time equal ![]() times
its earliest arrival.
Thus the hyperbolas shown depict only rays
moving within 45
times
its earliest arrival.
Thus the hyperbolas shown depict only rays
moving within 45![]() of the vertical.
It is good to remember this,
that the ratio of first arrival time on a hyperbola
to any other arrival time
gives the cosine of the angle of propagation.
The cutoff on each hyperbola is a ray at 45
of the vertical.
It is good to remember this,
that the ratio of first arrival time on a hyperbola
to any other arrival time
gives the cosine of the angle of propagation.
The cutoff on each hyperbola is a ray at 45![]() .Notice that the end points of the hyperbolas on the drawing
can be connected by a straight line.
Also, the slope at the end of each hyperbola is the same.
In physical space, the angle of any ray is
.Notice that the end points of the hyperbolas on the drawing
can be connected by a straight line.
Also, the slope at the end of each hyperbola is the same.
In physical space, the angle of any ray is
![]() .For any plane wave
(or seismic event that is near a plane wave),
the slope
.For any plane wave
(or seismic event that is near a plane wave),
the slope ![]() is
is ![]() ,as you can see by considering a wavefront intercepting the earth's surface
at angle
,as you can see by considering a wavefront intercepting the earth's surface
at angle ![]() .So, energy moving on a straight line in physical (x , z)-space
migrates along a straight line in data (x , t)-space.
As z increases, the energy of all angles comes together to a focus.
The focus is the exploding reflector.
It is the gap in the barrier.
This third definition of migration is that it is the
process that somehow pushes observational data--wave
height as a function of x and t --from the beach to the barrier.
The third definition stresses not so much the motion itself,
but the transformation from the beginning point to the ending point.
.So, energy moving on a straight line in physical (x , z)-space
migrates along a straight line in data (x , t)-space.
As z increases, the energy of all angles comes together to a focus.
The focus is the exploding reflector.
It is the gap in the barrier.
This third definition of migration is that it is the
process that somehow pushes observational data--wave
height as a function of x and t --from the beach to the barrier.
The third definition stresses not so much the motion itself,
but the transformation from the beginning point to the ending point.
To go further, a more general example is needed than the storm barrier example. The barrier example is confined to making Huygens sources only at some particular z. Sources are needed at other depths as well. Then, given a wave-extrapolation process to move data to increasing z values, exploding-reflector images are constructed with
| |
(2) |
| t = 0 | ||
| all |
||
Diffraction
is sometimes regarded as the natural process that creates and enlarges hyperboloids. Migration
is the computer process that does the reverse.
Another aspect of the use of the word migration arises where the horizontal coordinate can be either shot-to-geophone midpoint y, or offset h. Hyperboloids can be downward continued in both the (y , t)- and the (h , t)-plane. In the (y , t)-plane this is called migration or imaging, and in the (h , t)-plane it is called focusing or velocity analysis.