 |
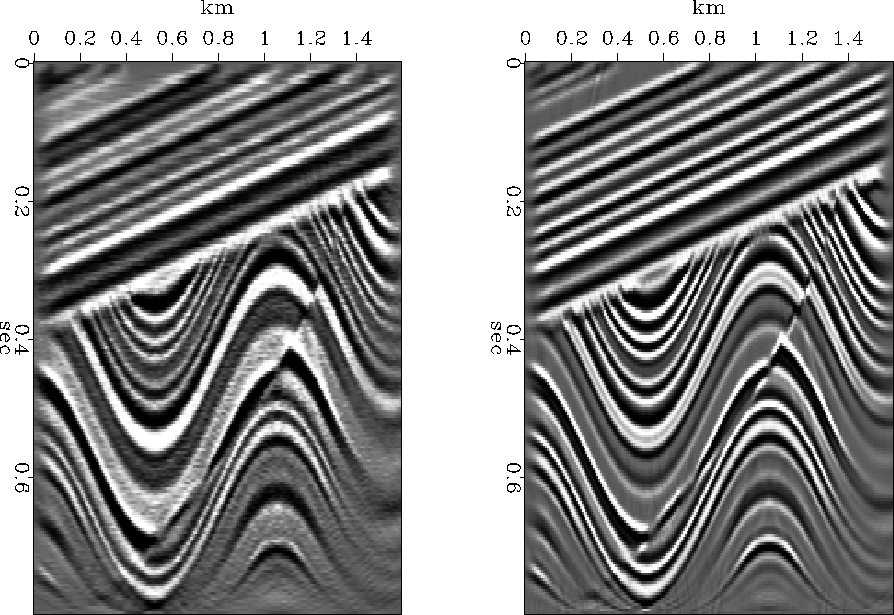
Figure 7 Reconstruction after modeling. Left is by the nearest-neighbor Kirchhoff method. Right is by the phase shift method.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we were introduced to the Kirchhoff
migration and modeling method by means of subroutines
kirchslow()
, we were introduced to the Kirchhoff
migration and modeling method by means of subroutines
kirchslow() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and kirchfast()
and kirchfast() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
From chapter
.
From chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we know that these routines should be
supplemented by a
we know that these routines should be
supplemented by a ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Here, however,
we will compare results of the unadorned subroutine kirchfast()
.
Here, however,
we will compare results of the unadorned subroutine kirchfast() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with our new programs, phasemig()
with our new programs, phasemig() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and phasemod()
and phasemod() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Figure 7 shows the result of modeling data and then migrating it.
Kirchhoff and phase-shift migration methods both work well.
As expected, the Kirchhoff method lacks some of the higher frequencies
that could be restored by
.
Figure 7 shows the result of modeling data and then migrating it.
Kirchhoff and phase-shift migration methods both work well.
As expected, the Kirchhoff method lacks some of the higher frequencies
that could be restored by ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
Figure 8 shows the temporal spectrum of the original sigmoid model,
along with the spectrum of the reconstruction via phase-shift methods.
We see the spectra are essentially identical
with little growth of high frequencies
as we noticed with the Kirchhoff method
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
|
phaspec
Figure 8 Top is the temporal spectrum of the model. Bottom is the spectrum of the reconstructed model. | 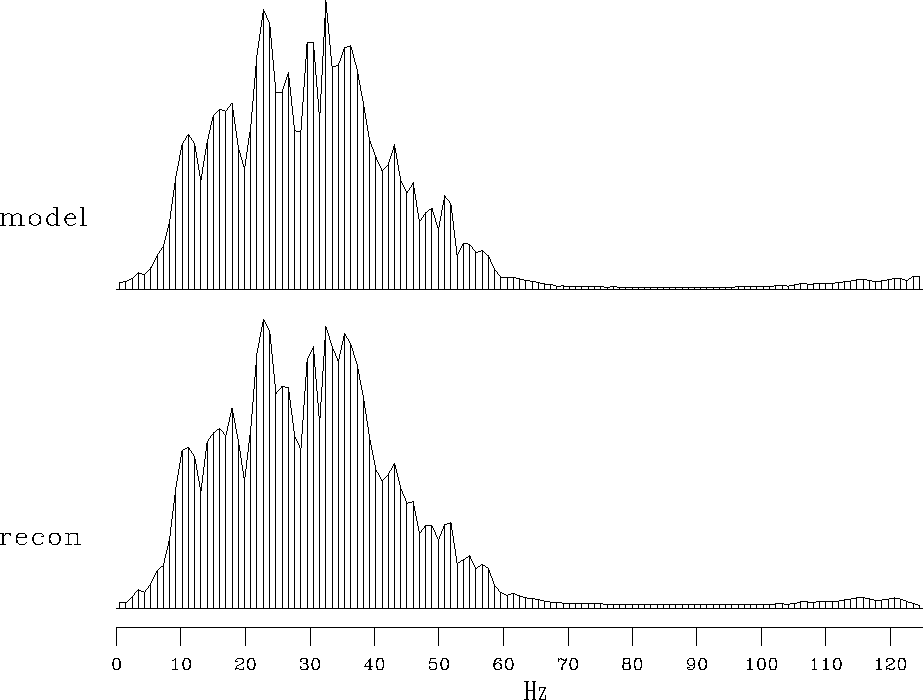 |
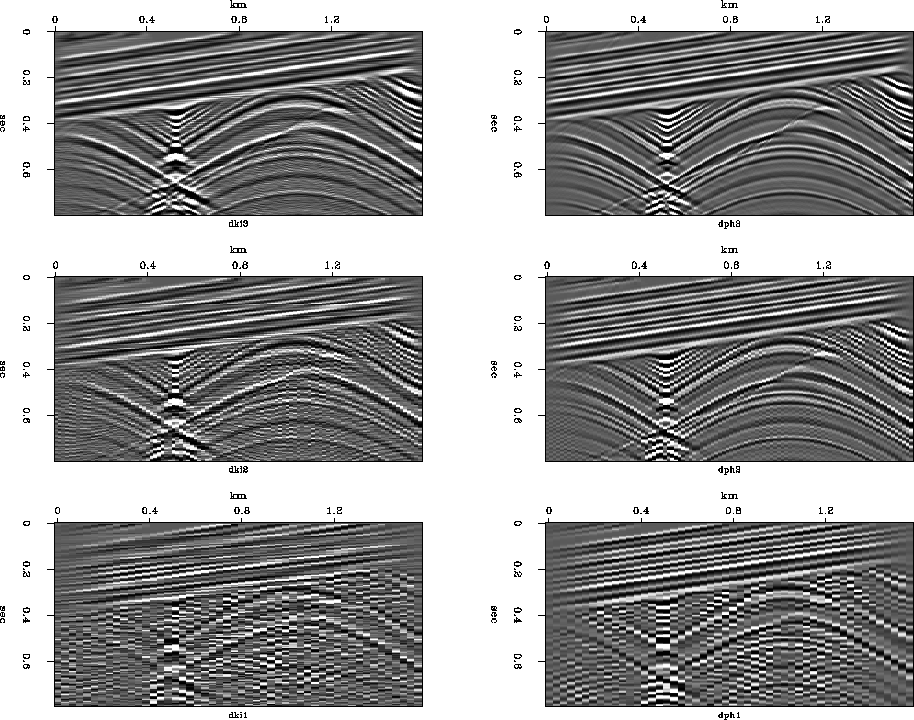
Figure 9 shows the effect of coarsening the space axis.
Synthetic data is generated from an increasingly subsampled model.
Again we notice that the phase-shift method of this chapter
produces more plausible results than
the simple Kirchhoff programs of chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |