|
frocca
Figure 18 Rocca's prestack partial-migration operator is a superposition of hyperbolas, each with its top on an ellipse. | 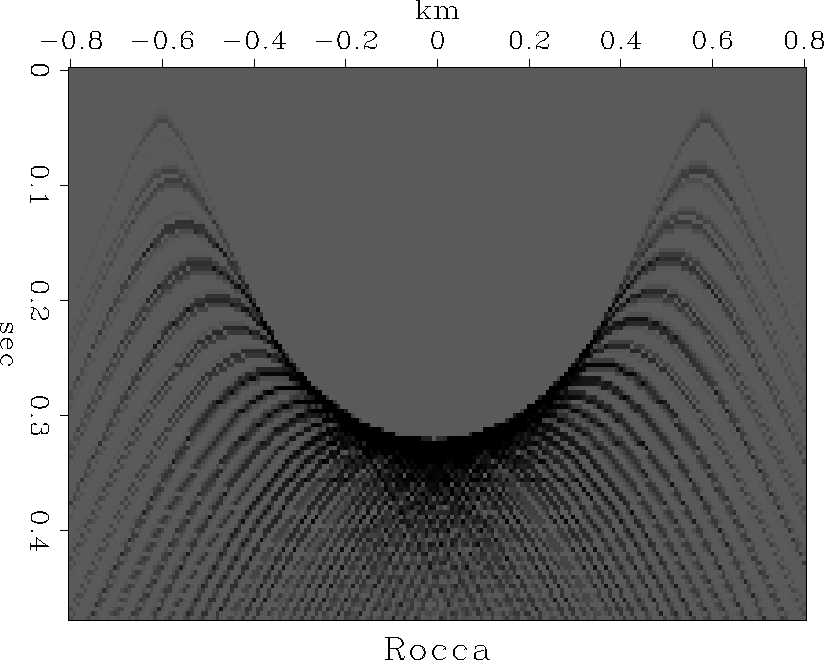 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) using some constant-offset h.
Although the result is an ellipsoidal curve,
think of it as a row of many points along an ellipsoidal curve.
Then diffract the image
thus turning each of the many points into a hyperbola.
We do this with the return path of the same subroutine flathyp(),
however the path back is taken with h=0.
The result is shown in Figure 18.
To enhance the appearance of the figure,
I injected an intermediate step of converting the ellipsoid
curve into a trajectory of dots on the ellipse.
Notice that the hyperbola tops
are not on the strong smear function that results
from the superposition.
using some constant-offset h.
Although the result is an ellipsoidal curve,
think of it as a row of many points along an ellipsoidal curve.
Then diffract the image
thus turning each of the many points into a hyperbola.
We do this with the return path of the same subroutine flathyp(),
however the path back is taken with h=0.
The result is shown in Figure 18.
To enhance the appearance of the figure,
I injected an intermediate step of converting the ellipsoid
curve into a trajectory of dots on the ellipse.
Notice that the hyperbola tops
are not on the strong smear function that results
from the superposition.
The strong smear function that you see in Figure 18 is Rocca's DMO+NMO operator, the operator that converts a point on a constant-offset section to a zero-offset section. The important feature of this operator is that the bulk of the energy is in a much narrower region than the big ellipse of migration. The narrowness of the Rocca operator is important since it means that energies will not move far, so the operator will not have a drastic effect and be unduly affected by remote data. (Being a small operator also makes it cheaper to apply). The little signals you see away from the central burst in Figure 18 result mainly from my modulating the ellipse curve into into a sequence of dots. However, noises from sampling and nearest-neighbor interpolation also yield a figure much like Figure 18. This warrants a more careful theoretical study to see how to represent the Rocca operator directly (rather than as a sequence of two nearly opposite operators).
|
frocca
Figure 18 Rocca's prestack partial-migration operator is a superposition of hyperbolas, each with its top on an ellipse. |  |
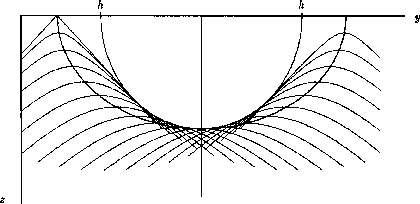
To get a sharper, more theoretical view of the Rocca operator,
Figure 19 shows line drawings of the curves in
a Rocca construction.
It happens, and we will later show,
that the Rocca operator lies along an ellipse
that passes through ![]() (and hence is independent of velocity!)
Curiously,
we see something we could not see on Figure 18,
that the Rocca curve ends part way up the ellipse
and it does not reach the surface.
The place where the Rocca operator ends
and the velocity independent ellipse continues is, however,
velocity dependent as we will see.
The Rocca operator is along the curve of osculation in Figure 19,
i.e., the smile-shaped curve where the hyperbolas reinforce one another.
(and hence is independent of velocity!)
Curiously,
we see something we could not see on Figure 18,
that the Rocca curve ends part way up the ellipse
and it does not reach the surface.
The place where the Rocca operator ends
and the velocity independent ellipse continues is, however,
velocity dependent as we will see.
The Rocca operator is along the curve of osculation in Figure 19,
i.e., the smile-shaped curve where the hyperbolas reinforce one another.
 |