 |
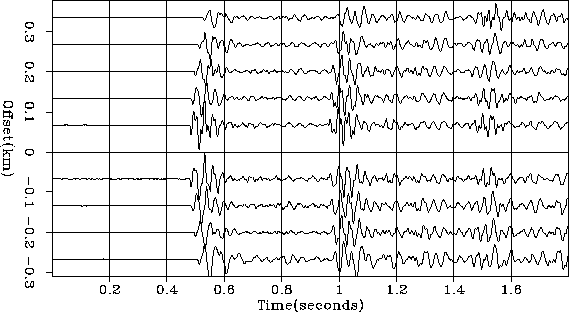
Figure 1 Some of the inner offset seismograms from Arctic dataset 24 (Yilmaz and Cumro).
 |
Apparently the initial waveform is somewhat complex, but the water-bottom reflection does not complicate it further. You can confirm this by noticing the water-bottom multiple reflection, i.e., the wave that bounces first from the water bottom, then from the water surface, and then a second time from the water bottom. This multiple reflection is similar to but has polarity opposite to the shape of the primary water-bottom reflection. (The opposite polarity results from the reflection at the ocean surface, where the acoustic pressure, the sum of the downgoing wave plus the upgoing wave, vanishes.)
Other data in water of similar depth shows a different reflection behavior. The bottom gives back not a single reflection, but a train of reflections. Let this train of reflections from the ocean floor be denoted by F(Z). Instead of looking like -F(Z), the first multiple reflection can look like -F(Z)2. The ray sketch in Figure 2 shows a simple multiple reflection.
|
peg
Figure 2 Water bottom soft-mud multiple (left) and similar travel times to mudstone (center and right). | 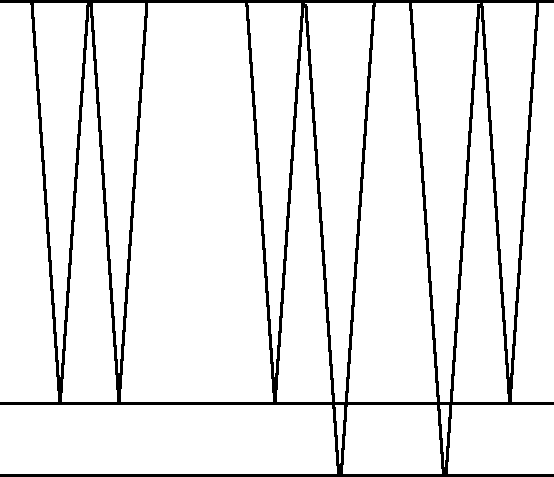 |
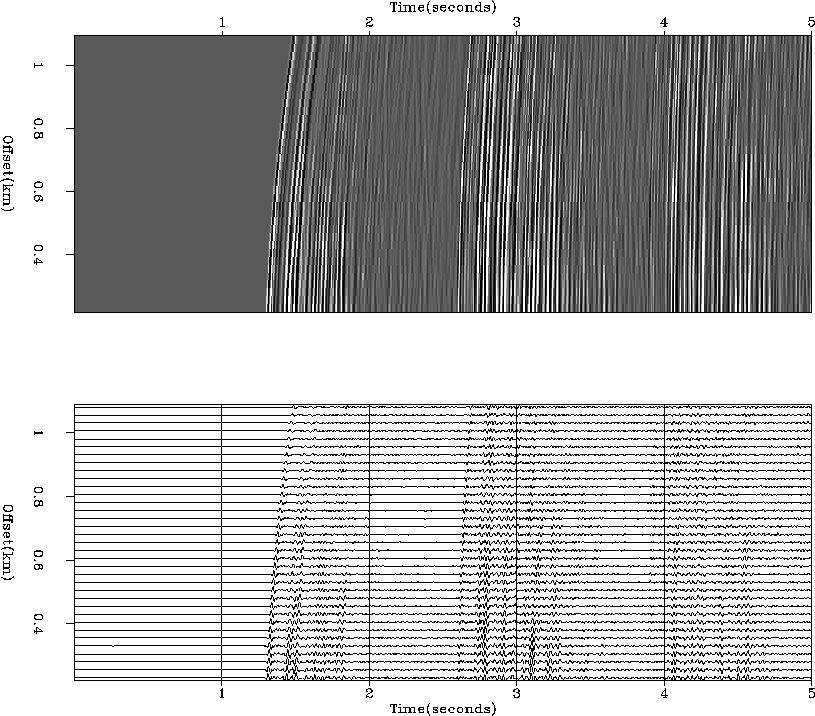 |
Figures 3 and 1 illustrate how arctic data typically contrasts with data from temperate or tropic regions. The arctic water-bottom reflection is generally hard, indicating that the bottom is in a constant state of erosion from the scraping of the ice floes and the carrying away of sediments by the bottom currents. In temperate and tropical climates, the bottom is often covered with soft sediments: the top layer is unconsolidated mud, and deeper layers are mud consolidated into mudstone.
Now we devise a simple mathematical model for the multiple reflections in Figures 1 and 3. There are two unknown waveforms, the source waveform S(Z) and the ocean-floor reflection F(Z). The water-bottom primary reflection P(Z) is the convolution of the source waveform with the water-bottom response; so P(Z)=S(Z)F(Z). The first multiple reflection M(Z) sees the same source waveform, the ocean floor, a minus one for the free surface, and the ocean floor again. Thus the observations P(Z) and M(Z) as functions of the physical parameters are
| |
(1) | |
| (2) |
| |
(3) | |
| (4) |
These solutions can be computed in the Fourier domain.
The difficulty is that the divisors in
equations (3) and (4)
can be zero, or small.
This difficulty can be attacked by using a positive number ![]() to stabilize it.
Equation (3), for example, could be written
to stabilize it.
Equation (3), for example, could be written
| |
(5) |
Functions that are rough in the frequency domain will be long in
the time domain.
This suggests making a short function in the time domain
by local smoothing in the frequency domain.
Let the notation ![]() denote smoothing by local averaging.
Thus we can specify filters whose time duration
is not unreasonably long by revising equation (5) to
denote smoothing by local averaging.
Thus we can specify filters whose time duration
is not unreasonably long by revising equation (5) to
| |
(6) |
These time-duration difficulties do not arise in a time-domain formulation. First express (3) and (4) as
| |
(7) | |
| (8) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Think of
).
Think of ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
theoretically.
With longer filters
we use numerical methods.
),
theoretically.
With longer filters
we use numerical methods.
In the time domain it is easy and natural
to limit the duration and location
of the nonzero coefficients in F(Z) and S(Z).
The required program for this task is
shaper(), which operates like
cgmeth() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
invstack()
and
invstack() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) except that
the operator needed here is contran()
except that
the operator needed here is contran() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
# shaping filter
# minimize SUM rr(i)**2 by finding ff and rr where
#
# rr = yy - xx (convolve) ff
#
subroutine shaper( nf,ff, nx,xx, ny, yy, rr, niter)
integer i, iter, nf, nx, ny, niter
real ff(nf), xx(nx), yy(ny), rr(ny)
temporary real df(nf), dr(ny), sf(nf), sr(ny)
if( ny != nx+nf-1) call erexit('data length error')
do i= 1, nf
ff(i) = 0.
do i= 1, ny
rr(i) = yy(i)
do iter= 0, niter {
call contran( 1, 0, nx,xx, nf,df, rr) # df=xx*rr
call contran( 0, 0, nx,xx, nf,df, dr) # dr=xx*df
call cgstep( iter, nf,ff,df,sf, ny,rr,dr,sr) # rr=rr-dr; ff=ff+df
}
return; end
The goal of finding the filters F(Z) and S(Z) is to best model the multiple reflections so that they can be subtracted from the data, enabling us to see what primary reflections have been hidden by the multiples. An important practical aspect is merging the analysis of many seismograms (see exercises).
Typical data includes not only that shown in Figures 1 and 3, but also wider source-receiver separation, as well as many other nearby shots and their receivers. Corrections need to be made for hyperbolic traveltime resulting from lateral separation between shot and receiver. Diffractions are a result of lateral imperfections in the generally flat sea floor. The spatial aspects of this topic are considered at great length in IEI. We will investigate them here in only a limited way.