Tent smoothing

First recall triangular smoothing in one dimension with subroutine triangle() . This routine is easily adapted to two dimensions. First we smooth in the direction of the 1-axis for all values of the 2-axis. Then we do the reverse, convolve on the 2-axis for all values of the 1-axis. Now recall that smoothing with a rectangle is especially fast, because we do not need to add all the points within the rectangle. We merely adapt a shifted rectangle by adding a point at one end and subtracting a point at the other end. In other words, the cost of smoothing is independent of the width of the rectangle. And no multiplies are required. To get a triangle, we smooth twice with rectangles.

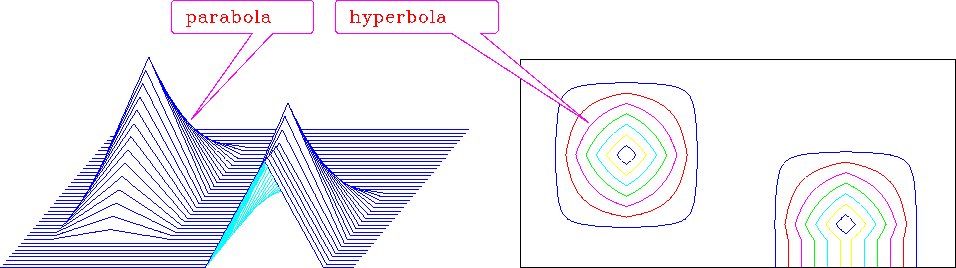
Figure 11 shows the application of triangle smoothers on two pulses in a plane. The plane was first convolved with a triangle on the 1-axis and then with another triangle on the 2-axis. This takes each impulse and smooths it into an interesting pyramid that I call a tent.

 

pyram
Figure 11 Two impulses in two dimensions filtered with a triangle function along each spatial axis. Left: bird's-eye view. Right: contours of constant altitude z.

The expected side-boundary effect is visible on the foreground tent. In the contour plot (of the same 120 by 40 mesh), we see that the cross section of the tent is rectangular near the base and diamond shaped near the top. The altitude of the jth tent face is z = a(x-x_j)(y-y_j), where (x_j, y_j) is the location of a corner and a is a scale. The tent surface is parabolic (like z=x²) along x=y but linear along lines parallel to the axes. A contour of constant z is the (hyperbolic) curve y = a+b/(x+c) (where a, b, and c are different constants on each of the four faces).