




Next: References
Up: Introduction
Previous: Linear inverse theory
Centrally, this book teaches
how to recognize adjoint operators
in physical processes (chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and how to use those adjoints in model fitting (inversion)
using least-squares optimization
and the technique of conjugate gradients (chapter
),
and how to use those adjoints in model fitting (inversion)
using least-squares optimization
and the technique of conjugate gradients (chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
First, however, we review
convolution and spectra
(chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
discrete Fourier transforms (chapter
)
discrete Fourier transforms (chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and causality and the complex
),
and causality and the complex
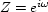 plane (chapter
plane (chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
where poles are the mathematically forbidden points of zero division.
In chapter
),
where poles are the mathematically forbidden points of zero division.
In chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we travel widely,
from the heaven of theoretically perfect results
through a life of practical results including poor results,
sinking to the purgatory of instability,
and finally arriving at the ``big bang'' of zero division.
Chapter
we travel widely,
from the heaven of theoretically perfect results
through a life of practical results including poor results,
sinking to the purgatory of instability,
and finally arriving at the ``big bang'' of zero division.
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a collection of solved problems
with a single unknown that illustrates the pitfalls and opportunities
that arise from weighting functions, zero division, and nonstationarity.
Thus we are prepared for the keystone chapter, chapter
is a collection of solved problems
with a single unknown that illustrates the pitfalls and opportunities
that arise from weighting functions, zero division, and nonstationarity.
Thus we are prepared for the keystone chapter, chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
where we learn to recognize the relation of the linear operators
we studied in chapters 1-3 to their adjoints,
and to see how computation of these adjoints
is a straightforward adjunct to direct computation.
Also included in chapter
,
where we learn to recognize the relation of the linear operators
we studied in chapters 1-3 to their adjoints,
and to see how computation of these adjoints
is a straightforward adjunct to direct computation.
Also included in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are interpolation, smoothing,
and most of the many operators that populate the world of
exploration seismology.
Thus further prepared,
we pass easily through the central theoretical
concepts of least-squares optimization,
basic NMO stack,
and deconvolution applications
in chapter
are interpolation, smoothing,
and most of the many operators that populate the world of
exploration seismology.
Thus further prepared,
we pass easily through the central theoretical
concepts of least-squares optimization,
basic NMO stack,
and deconvolution applications
in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
In chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we see the formulation and solution
of many problems in time-series analysis,
prediction, and interpolation and learn
more about mathematical formulations that control stability.
Chapter
we see the formulation and solution
of many problems in time-series analysis,
prediction, and interpolation and learn
more about mathematical formulations that control stability.
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how missing data can be estimated.
Of particular interest is a nonstationary world model where,
locally in time and space,
the wave field fits the model of a small number of plane waves.
Here we find ``magical'' results:
data that is apparently undersampled (spatially aliased)
is recovered.
shows how missing data can be estimated.
Of particular interest is a nonstationary world model where,
locally in time and space,
the wave field fits the model of a small number of plane waves.
Here we find ``magical'' results:
data that is apparently undersampled (spatially aliased)
is recovered.
Hyperbolas are the reflection seismologist's delight.
My book
could almost have been named
Hyperbolas and the Earth.
That book includes many techniques for representing and deforming hyperbolas,
especially using various representations of the wave equation.
Here I repeat a minimal part of that lore in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
My goal is now to marry hyperbolas
to the conjugate-gradient model-fitting theme of this book.
.
My goal is now to marry hyperbolas
to the conjugate-gradient model-fitting theme of this book.
Having covered a wide range of practical problems,
we turn at last to more theoretical ones:
spectra and phase (chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and sample spectra of random numbers (chapter
),
and sample spectra of random numbers (chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
I have begun revising
three theoretical chapters
from my first book,
(hereinafter referred to as FGDP),
which is still in print.
Since these revisions are not yet very extensive,
I am excluding the revised chapters
from the current copy of this book.
(My 1985 book,
(hereinafter referred to as IEI),
deserves revision in the light of the conjugacy methods developed here,
but that too lies in the future.)
).
I have begun revising
three theoretical chapters
from my first book,
(hereinafter referred to as FGDP),
which is still in print.
Since these revisions are not yet very extensive,
I am excluding the revised chapters
from the current copy of this book.
(My 1985 book,
(hereinafter referred to as IEI),
deserves revision in the light of the conjugacy methods developed here,
but that too lies in the future.)
Finally, every academic is entitled to some idiosyncrasies,
and I find Jensen inequalities fascinating.
These have an unproved relationship to practical echo analysis,
but I include them anyway in a brief concluding chapter.





Next: References
Up: Introduction
Previous: Linear inverse theory
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
discrete Fourier transforms (chapter
)
discrete Fourier transforms (chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and causality and the complex
),
and causality and the complex
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
where poles are the mathematically forbidden points of zero division.
In chapter
),
where poles are the mathematically forbidden points of zero division.
In chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we travel widely,
from the heaven of theoretically perfect results
through a life of practical results including poor results,
sinking to the purgatory of instability,
and finally arriving at the ``big bang'' of zero division.
Chapter
we travel widely,
from the heaven of theoretically perfect results
through a life of practical results including poor results,
sinking to the purgatory of instability,
and finally arriving at the ``big bang'' of zero division.
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a collection of solved problems
with a single unknown that illustrates the pitfalls and opportunities
that arise from weighting functions, zero division, and nonstationarity.
Thus we are prepared for the keystone chapter, chapter
is a collection of solved problems
with a single unknown that illustrates the pitfalls and opportunities
that arise from weighting functions, zero division, and nonstationarity.
Thus we are prepared for the keystone chapter, chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
where we learn to recognize the relation of the linear operators
we studied in chapters 1-3 to their adjoints,
and to see how computation of these adjoints
is a straightforward adjunct to direct computation.
Also included in chapter
,
where we learn to recognize the relation of the linear operators
we studied in chapters 1-3 to their adjoints,
and to see how computation of these adjoints
is a straightforward adjunct to direct computation.
Also included in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are interpolation, smoothing,
and most of the many operators that populate the world of
exploration seismology.
Thus further prepared,
we pass easily through the central theoretical
concepts of least-squares optimization,
basic NMO stack,
and deconvolution applications
in chapter
are interpolation, smoothing,
and most of the many operators that populate the world of
exploration seismology.
Thus further prepared,
we pass easily through the central theoretical
concepts of least-squares optimization,
basic NMO stack,
and deconvolution applications
in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.