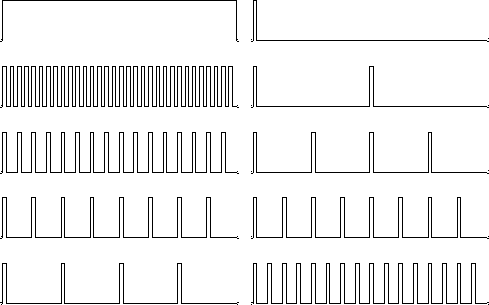Consider a constant function of time. In the frequency domain, it is an impulse at zero frequency. The comb function is defined to be zero at alternate time points. Multiply this constant function by the comb function. The resulting signal contains equal amounts of two frequencies; half is zero frequency, and half is Nyquist frequency. We see this in the second row in Figure 2, where the Nyquist energy is in the middle of the frequency axis. In the third row, 3 out of 4 points are zeroed by another comb. We now see something like a new Nyquist frequency at half the Nyquist frequency visible on the second row.
|
comb
Figure 1 A zero-frequency function and its cosine transform. Successive rows show increasingly sparse sampling of the zero-frequency function. |  |
