




Next: Stability of the explicit
Up: Splitting and working in
Previous: (t,x,z)-Space, 45 degree equation
Experience shows that as soon as you undertake an application
that departs significantly from textbook situations,
stability becomes a greater concern than accuracy.
Stability, or its absence, determines whether the goal is
achievable at all, whereas accuracy merely determines the price
of achieving it.
Here we will look at the stability of the heat-flow equation with
real and with imaginary heat conductivity.
Since the latter case corresponds to seismic migration, these two
cases provide a useful background for stability analysis.
Most stability analysis is based on Fourier transformation.
More simply, single sinusoidal or complex exponential
trial solutions are examined.
If a method becomes unstable for any frequency,
then it will be unstable for any realistic case,
because realistic functions
are just combinations of all frequencies.
Begin with the sinusoidal function
| 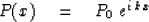 |
(62) |
The second derivative is
| 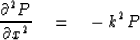 |
(63) |
An expression analogous to the second difference operator defines 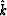 :
:
| 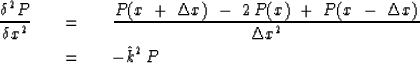 |
(64) |
| (65) |
Ideally 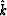 should equal k.
Inserting the complex exponential (62) into (64) gives
an expression for
should equal k.
Inserting the complex exponential (62) into (64) gives
an expression for 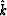 :
:
| ![\begin{eqnarray}
-\ \hat k^2 \,P \ \ \ &=&\ \ \ { P_0 \over \Delta x^2 } \
\lef...
... k \,\Delta x )^2 \ \ \ &=&\ \ \ 2 \ [ 1\ -\ \cos ( k \Delta x ) ]\end{eqnarray}](img137.gif) |
(66) |
| (67) |
It is a straightforward matter to make plots of (67)
or its square root.
The square root of (67),
through the half-angle trig identity, is
| 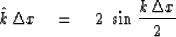 |
(68) |
Series expansion shows
that 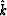 matches k well at low spatial frequencies.
At the Nyquist frequency, defined by
matches k well at low spatial frequencies.
At the Nyquist frequency, defined by 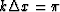 ,the value of
,the value of 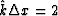 is a poor approximation to
is a poor approximation to  .As with any Fourier transform on the discrete domain,
.As with any Fourier transform on the discrete domain, 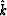 is a
periodic function of k above the Nyquist frequency.
Although k ranges from minus infinity
to plus infinity,
is a
periodic function of k above the Nyquist frequency.
Although k ranges from minus infinity
to plus infinity, 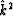 is compressed into the range zero to four.
The limits to the range are important since instability often starts
at one end of the range.
is compressed into the range zero to four.
The limits to the range are important since instability often starts
at one end of the range.





Next: Stability of the explicit
Up: Splitting and working in
Previous: (t,x,z)-Space, 45 degree equation
Stanford Exploration Project
10/31/1997
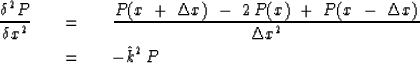
![\begin{eqnarray}
-\ \hat k^2 \,P \ \ \ &=&\ \ \ { P_0 \over \Delta x^2 } \
\lef...
... k \,\Delta x )^2 \ \ \ &=&\ \ \ 2 \ [ 1\ -\ \cos ( k \Delta x ) ]\end{eqnarray}](img137.gif)