




Next: INTERVAL VELOCITY BY LINEAR
Up: SNELL WAVES AND SKEWED
Previous: Snell wave coordinates
The chain rule for partial differentiation says that
| ![\begin{displaymath}
\left[ \
\matrix { \partial_t \cr \partial_x \cr \partial_z...
...tial_{ t' } \cr \partial_{{x}' }
\cr \partial_{{z}' } }
\right]\end{displaymath}](img83.gif) |
(35) |
In Fourier space, the top two rows of the above matrix may be interpreted as
| 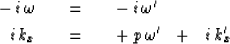 |
(36) |
| (37) |
Of particular interest is the energy that is flat
after linear moveout (constant with x').
For such energy 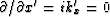 .Combining (36) and (37) gives the familiar equation
.Combining (36) and (37) gives the familiar equation
| 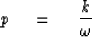 |
(38) |
EXERCISES:
-
Explain the choice of sign of the s-axis in Figure 11.
-
Equations (30), (31) and (32) are for
upgoing
Snell waves.
What coordinate system would be appropriate for
downgoing
Snell waves?
-
Express the scalar wave equation in the coordinate system
(30), (31) and (32).
Neglect first derivatives.
-
Express the dispersion relation of the scalar wave equation in terms of the
Fourier variables
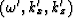 .
.





Next: INTERVAL VELOCITY BY LINEAR
Up: SNELL WAVES AND SKEWED
Previous: Snell wave coordinates
Stanford Exploration Project
10/31/1997
![\begin{displaymath}
\left[ \
\matrix { \partial_t \cr \partial_x \cr \partial_z...
...tial_{ t' } \cr \partial_{{x}' }
\cr \partial_{{z}' } }
\right]\end{displaymath}](img83.gif)
![\begin{displaymath}
\left[ \
\matrix { \partial_t \cr \partial_x \cr \partial_z...
...tial_{ t' } \cr \partial_{{x}' }
\cr \partial_{{z}' } }
\right]\end{displaymath}](img83.gif)