




Next: Splitting diffraction and lens
Up: WAVE-EXTRAPOLATION EQUATIONS
Previous: Lateral velocity variation
You may wonder where the two velocities v(x,z) and 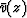 came from.
The first arises in the wave equation,
and it must be x-variable if the model is x-variable.
The second arises in a mathematical transformation,
namely, equation (15),
so it is purely a matter of definition.
Experience shows that complications will abound if we try to make
the defined velocity
came from.
The first arises in the wave equation,
and it must be x-variable if the model is x-variable.
The second arises in a mathematical transformation,
namely, equation (15),
so it is purely a matter of definition.
Experience shows that complications will abound if we try to make
the defined velocity 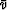 depend on x.
But it is nice if the two velocities can be equal
so the term containing their difference drops out of the analysis.
Thus ordinarily,
depend on x.
But it is nice if the two velocities can be equal
so the term containing their difference drops out of the analysis.
Thus ordinarily, 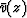 is chosen
to be some kind of horizontal average of v (x,z).
is chosen
to be some kind of horizontal average of v (x,z).





Next: Splitting diffraction and lens
Up: WAVE-EXTRAPOLATION EQUATIONS
Previous: Lateral velocity variation
Stanford Exploration Project
10/31/1997