




Next: Lateral velocity variation
Up: WAVE-EXTRAPOLATION EQUATIONS
Previous: Depth-variable velocity
It is often convenient to arrange the calculation of a wave
to remove the effect of overall translation,
thereby making the wave appear to ``stand still.''
This subject, wave retardation,
will be examined more thoroughly in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Meanwhile, it is easy enough to introduce
the time shift t0 of a vertically propagating wave
in a hypothetical medium of velocity
.
Meanwhile, it is easy enough to introduce
the time shift t0 of a vertically propagating wave
in a hypothetical medium of velocity 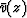 , namely,
, namely,
| 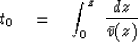 |
(14) |
A time delay t0 in
the time domain corresponds to multiplication
by 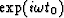 in the
in the 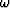 -domain.
Thus, the wave pressure P is related
to the time-shifted mathematical variable Q by
-domain.
Thus, the wave pressure P is related
to the time-shifted mathematical variable Q by
| 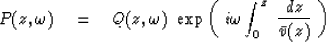 |
(15) |
which is a generalization of equation (3)
to depth-variable velocity.
(Equations (15) and (17) apply in both x- and
kx-space).
Differentiating with respect to z gives
| 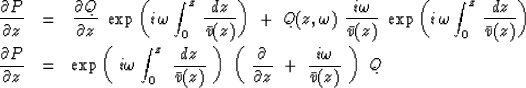 |
(16) |
| (17) |
Next, substitute (15) and (17)
into Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .3
to obtain the retarded equations in Table
.3
to obtain the retarded equations in Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4.
.4.
Table 4:
Retarded form of phase-shift equations.
| |
|
|
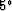 |
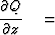 zero zero |
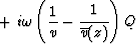 |
| |
|
|
| |
|
|
 |
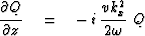 |
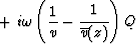 |
| |
|
|
| |
|
|
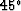 |
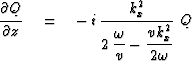 |
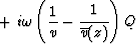 |
| |
|
|
| |
|
|
| general |
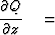 diffraction diffraction |
+ thin lens |
| |
|
|





Next: Lateral velocity variation
Up: WAVE-EXTRAPOLATION EQUATIONS
Previous: Depth-variable velocity
Stanford Exploration Project
10/31/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Meanwhile, it is easy enough to introduce
the time shift t0 of a vertically propagating wave
in a hypothetical medium of velocity
.
Meanwhile, it is easy enough to introduce
the time shift t0 of a vertically propagating wave
in a hypothetical medium of velocity ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Meanwhile, it is easy enough to introduce
the time shift t0 of a vertically propagating wave
in a hypothetical medium of velocity
.
Meanwhile, it is easy enough to introduce
the time shift t0 of a vertically propagating wave
in a hypothetical medium of velocity ![]() , namely,
, namely,
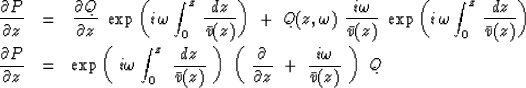
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .3
to obtain the retarded equations in Table
.3
to obtain the retarded equations in Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4.
.4.