




Next: Waves in Fourier space
Up: PLANE-WAVE SUPERPOSITION
Previous: Migration improves horizontal resolution
Figure 4 depicts a ray moving down into the earth
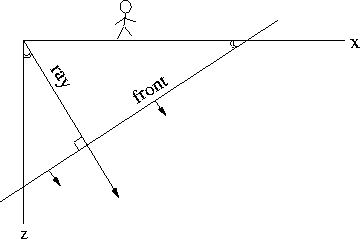
at an angle 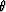 from the vertical.
from the vertical.
front
Figure 4
Downgoing ray and wavefront.
|
|  |

Perpendicular to the ray is a wavefront.
By elementary geometry the angle between the wavefront and the earth's surface
is also 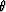 .The ray increases its length at a speed v.
The speed that is observable on the earth's surface is the intercept
of the wavefront with the earth's surface.
This speed, namely
.The ray increases its length at a speed v.
The speed that is observable on the earth's surface is the intercept
of the wavefront with the earth's surface.
This speed, namely 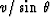 , is faster than v.
Likewise, the speed of the intercept of the wavefront and
the vertical axis is
, is faster than v.
Likewise, the speed of the intercept of the wavefront and
the vertical axis is 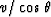 .A mathematical expression for a straight line would be
.A mathematical expression for a straight line would be
| 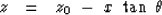 |
(1) |
like that shown to be the wavefront
in Figure 4.
In this expression z0 is the intercept between the wavefront
and the vertical axis.
To make the intercept move downward, replace it by the
appropriate velocity times time:
| 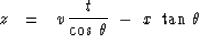 |
(2) |
Solving for time gives
| 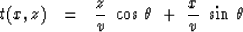 |
(3) |
Equation (3) tells the time that the wavefront will pass any
particular location (x , z).
The expression for a shifted waveform
of arbitrary shape is 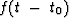 .Using (3) to define the time shift t0 gives an expression for
a wavefield that is some waveform moving on a ray.
.Using (3) to define the time shift t0 gives an expression for
a wavefield that is some waveform moving on a ray.
| 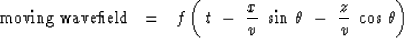 |
(4) |





Next: Waves in Fourier space
Up: PLANE-WAVE SUPERPOSITION
Previous: Migration improves horizontal resolution
Stanford Exploration Project
10/31/1997
![]() from the vertical.
from the vertical.

![]() .The ray increases its length at a speed v.
The speed that is observable on the earth's surface is the intercept
of the wavefront with the earth's surface.
This speed, namely
.The ray increases its length at a speed v.
The speed that is observable on the earth's surface is the intercept
of the wavefront with the earth's surface.
This speed, namely ![]() , is faster than v.
Likewise, the speed of the intercept of the wavefront and
the vertical axis is
, is faster than v.
Likewise, the speed of the intercept of the wavefront and
the vertical axis is ![]() .A mathematical expression for a straight line would be
.A mathematical expression for a straight line would be