




Next: Stepping in depth
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: Viscosity and causality
The kz square root may be computed with the square root function
in your computer or by Muir's expansion.
For Fourier domain calculations incorporating causality,
you must use a complex square root function.
This will also take care of the
evanescent region automatically--you no longer have the discontinuity
between evanescent and nonevanescent regions.
The square root of a complex number is multivalued,
so you better first check that your computer
chooses the phase as described in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Mine did.
But I found that limited numerical accuracy prevented me from
achieving strict positivity of the real part of the impedance
until I replaced the expression
.
Mine did.
But I found that limited numerical accuracy prevented me from
achieving strict positivity of the real part of the impedance
until I replaced the expression 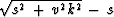 by
its algebraic
equivalent
by
its algebraic
equivalent 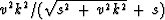 .
.
For finite differencing we will need the Muir recurrence.
Let r0 define the cosine of the angle that starts
the Muir recurrence, often 0 or 45
or 45 .This is another free parameter for optimization.
This angle is also an angle of exact fit
for all orders of the recurrence.
.This is another free parameter for optimization.
This angle is also an angle of exact fit
for all orders of the recurrence.
|  |
(52) |
Starting from 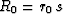 the Muir recursion is
equation (53):
the Muir recursion is
equation (53):
| 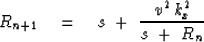 |
(53) |
For a diffraction program we will be evaluating 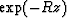 .Since R can be proven to have a positive real part,
the exponential should never grow.
Finite difference calculations are normally done with retarded time.
To retard time,
.Since R can be proven to have a positive real part,
the exponential should never grow.
Finite difference calculations are normally done with retarded time.
To retard time, 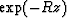 is expressed as
is expressed as
| 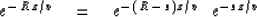 |
(54) |
As discussed earlier in this chapter,
you probably don't want the time shift of retardation
to be associated with viscous effects.
So you will probably want to downward continue instead with
| ![\begin{displaymath}
e^{ -\,[ R( -i \hat \omega ) \,+\, i \hat \omega ]\,z/v } \ \
e^{ + i \omega\,z/v}\end{displaymath}](img151.gif) |
(55) |
Notice the signs and distinction of 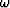 from
from 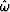 .
.
From equation (53)
we see that R-s should have a positive real part.
I found that numerical roundoff sometimes prevented it.
So the Muir recurrence was reorganized to incorporate the retardation.
Let
|  |
(56) |
Equation (53) becomes
| 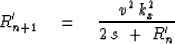 |
(57) |
From Muir's rules,
you can see that R ' will always have a positive real part
if we start it that way, so we start it from
| 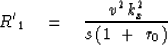 |
(58) |
(Combining (58) and (56)
gives the same 15 equation as does (53).)
Mathematically (55) is identical to
equation as does (53).)
Mathematically (55) is identical to
| 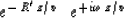 |
(59) |
but numerically the exponential in (59) is assured to decay in z.





Next: Stepping in depth
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: Viscosity and causality
Stanford Exploration Project
10/31/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Mine did.
But I found that limited numerical accuracy prevented me from
achieving strict positivity of the real part of the impedance
until I replaced the expression
.
Mine did.
But I found that limited numerical accuracy prevented me from
achieving strict positivity of the real part of the impedance
until I replaced the expression ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Mine did.
But I found that limited numerical accuracy prevented me from
achieving strict positivity of the real part of the impedance
until I replaced the expression
.
Mine did.
But I found that limited numerical accuracy prevented me from
achieving strict positivity of the real part of the impedance
until I replaced the expression ![]() by
its algebraic
equivalent
by
its algebraic
equivalent ![]() .
.![]() or 45
or 45![]() .This is another free parameter for optimization.
This angle is also an angle of exact fit
for all orders of the recurrence.
.This is another free parameter for optimization.
This angle is also an angle of exact fit
for all orders of the recurrence.
![]() .Since R can be proven to have a positive real part,
the exponential should never grow.
Finite difference calculations are normally done with retarded time.
To retard time,
.Since R can be proven to have a positive real part,
the exponential should never grow.
Finite difference calculations are normally done with retarded time.
To retard time, ![]() is expressed as
is expressed as