Next: REFERENCES
Up: Nonstationarity: patching
Previous: The human eye as
time-variable deconvolution
deconvolution ! time-variable
filter ! time-variable
Filters sometimes change with time and space.
We sometimes observe signals whose spectrum changes with position.
A filter that changes with position is called nonstationary.
We need an extension of our usual convolution operator
hconest ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Conceptually,
little needs to be changed besides changing
aa(ia) to
aa(ia,iy).
But there is a practical problem.
Fomel and I have made the decision
to clutter up the code somewhat
to save a great deal of memory.
This should be important to people interested in
solving multidimensional problems with big data sets.
.
Conceptually,
little needs to be changed besides changing
aa(ia) to
aa(ia,iy).
But there is a practical problem.
Fomel and I have made the decision
to clutter up the code somewhat
to save a great deal of memory.
This should be important to people interested in
solving multidimensional problems with big data sets.
Normally, the number of filter coefficients is many fewer
than the number of data points,
but here we have very many more.
Indeed, there are na times more.
Variable filters require na times more memory than the data itself.
To make the nonstationary helix code more practical,
we now require the filters to be constant in patches.
The data type for nonstationary filters
(which are constant in patches)
is introduced in module
nhelix, which is a simple modification of module
helix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
nhelixnon-stationary convolution
What is new is the integer valued vector pch(nd)
the size of the one-dimensional (helix) output data space.
Every filter output point is to be assigned to a patch.
All filters of a given patch number will be the same filter.
Nonstationary helixes are created with
createnhelixmod, which is a simple modification of module
createhelixmod
.
nhelixnon-stationary convolution
What is new is the integer valued vector pch(nd)
the size of the one-dimensional (helix) output data space.
Every filter output point is to be assigned to a patch.
All filters of a given patch number will be the same filter.
Nonstationary helixes are created with
createnhelixmod, which is a simple modification of module
createhelixmod ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
createnhelixmodcreate non-stationary helix
Notice that the user must define the pch(product(nd))
vector before creating a nonstationary helix.
For a simple 1-D time-variable filter,
presumably pch would be something like
.
createnhelixmodcreate non-stationary helix
Notice that the user must define the pch(product(nd))
vector before creating a nonstationary helix.
For a simple 1-D time-variable filter,
presumably pch would be something like
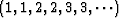 .For multidimensional patching we need to think a little more.
.For multidimensional patching we need to think a little more.
Finally, we are ready for the convolution operator.
The operator nhconest ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) allows for a different filter in each patch.
nhconestnon-stationary convolution
A filter output y(iy)
has its filter from the patch ip=aa%pch(iy).
The line
t=a(ip,:)
extracts the filter for the ipth patch.
If you are confused (as I am) about the difference
between aa and a,
maybe now is the time to have a look at beyond Loptran
to the Fortran version.
allows for a different filter in each patch.
nhconestnon-stationary convolution
A filter output y(iy)
has its filter from the patch ip=aa%pch(iy).
The line
t=a(ip,:)
extracts the filter for the ipth patch.
If you are confused (as I am) about the difference
between aa and a,
maybe now is the time to have a look at beyond Loptran
to the Fortran version.![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Because of the massive increase in the number of filter coefficients,
allowing these many filters
takes us from overdetermined to very undetermined.
We can estimate all these filter coefficients
by the usual deconvolution fitting goal (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
| 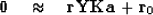 |
(21) |
but we need to supplement it with some damping goals, say
| 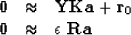 |
(22) |
where 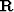 is a roughening operator to be chosen.
is a roughening operator to be chosen.
Experience with missing data in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that when the roughening operator
shows that when the roughening operator 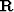 is a differential operator,
the number of iterations can be large.
We can speed the calculation immensely by ``preconditioning''.
Define a new variable
is a differential operator,
the number of iterations can be large.
We can speed the calculation immensely by ``preconditioning''.
Define a new variable 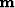 by
by
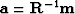 and insert it into (22) to get
the equivalent preconditioned system of goals.
and insert it into (22) to get
the equivalent preconditioned system of goals.
| 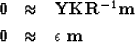 |
(23) |
| (24) |
The fitting (23) uses the operator 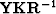 .For
.For 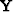 we can use subroutine
nhconest()
we can use subroutine
nhconest() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ;
for the smoothing operator
;
for the smoothing operator 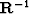 we can use nonstationary
polynomial division
with operator npolydiv():
npolydivnon-stationary polynomial division
Now we have all the pieces we need.
As we previously estimated stationary filters with
the module pef
we can use nonstationary
polynomial division
with operator npolydiv():
npolydivnon-stationary polynomial division
Now we have all the pieces we need.
As we previously estimated stationary filters with
the module pef ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
now we can estimate nonstationary PEFs with
the module npef
,
now we can estimate nonstationary PEFs with
the module npef ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The steps are hardly any different.
npefnon-stationary PEF
Near the end
of module npef
is a filter reshape
from a 1-D array to a 2-D array.
If you find it troublesome that
nhconest
.
The steps are hardly any different.
npefnon-stationary PEF
Near the end
of module npef
is a filter reshape
from a 1-D array to a 2-D array.
If you find it troublesome that
nhconest ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) was using the filter
during the optimization as already multidimensional,
perhaps again,
it is time to examine the Fortran code.
The answer is that there has been a conversion
back and forth partially hidden by Loptran.
was using the filter
during the optimization as already multidimensional,
perhaps again,
it is time to examine the Fortran code.
The answer is that there has been a conversion
back and forth partially hidden by Loptran.
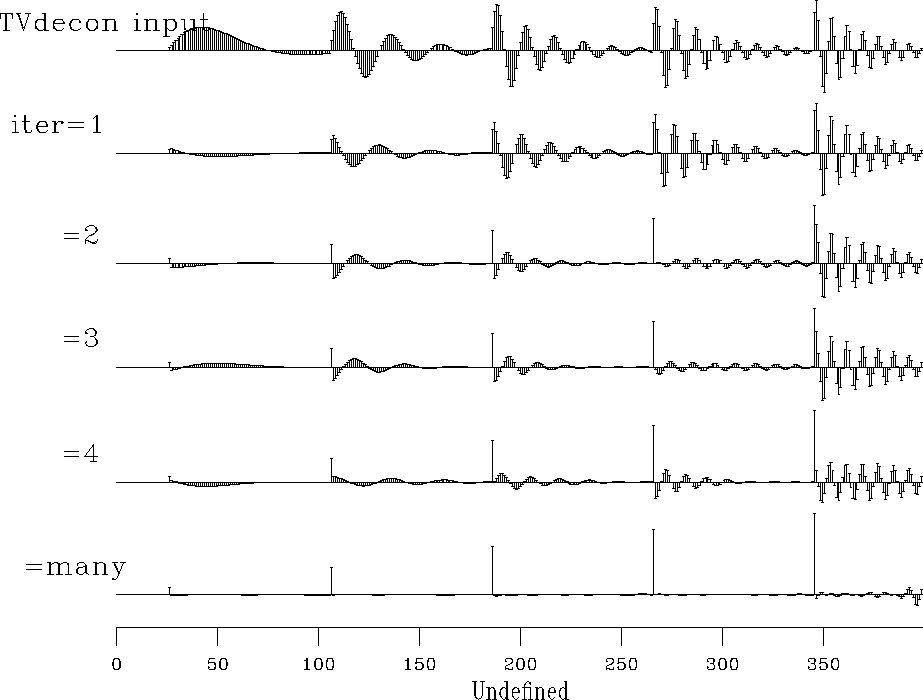
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a synthetic data example using these programs.
As we hope for deconvolution, events are compressed.
The compression is fairly good, even though each event has
a different spectrum.
What is especially pleasing is that satisfactory results
are obtained in truly small numbers of iterations (about three).
The example is for two free filter coefficients (1,a1,a2)
per output point.
The roughening operator
shows a synthetic data example using these programs.
As we hope for deconvolution, events are compressed.
The compression is fairly good, even though each event has
a different spectrum.
What is especially pleasing is that satisfactory results
are obtained in truly small numbers of iterations (about three).
The example is for two free filter coefficients (1,a1,a2)
per output point.
The roughening operator 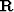 was taken to be (1,-2,1)
which was factored into
causal and anticausal finite difference.
was taken to be (1,-2,1)
which was factored into
causal and anticausal finite difference.
tvdecon90
Figure 15
Time variable deconvolution with
two free filter coefficients and a gap of 6.





I hope also to find a test case with field data,
but experience in seismology
is that spectral changes are slow,
which implies unexciting results.
Many interesting examples should exist
in two- and three-dimensional filtering, however,
because reflector dip is always changing
and that changes the spatial spectrum.
In multidimensional space, the smoothing filter 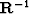 can be chosen with interesting directional properties.
Sergey, Bob, Sean and I have joked about this code being
the ``double helix'' program because there are two multidimensional
helixes in it, one the smoothing filter, the other the deconvolution filter.
Unlike the biological helixes, however, these two helixes
do not seem to form a symmetrical pair.
can be chosen with interesting directional properties.
Sergey, Bob, Sean and I have joked about this code being
the ``double helix'' program because there are two multidimensional
helixes in it, one the smoothing filter, the other the deconvolution filter.
Unlike the biological helixes, however, these two helixes
do not seem to form a symmetrical pair.






Next: REFERENCES
Up: Nonstationarity: patching
Previous: The human eye as
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
nhelixnon-stationary convolution
What is new is the integer valued vector pch(nd)
the size of the one-dimensional (helix) output data space.
Every filter output point is to be assigned to a patch.
All filters of a given patch number will be the same filter.
Nonstationary helixes are created with
createnhelixmod, which is a simple modification of module
createhelixmod
.
nhelixnon-stationary convolution
What is new is the integer valued vector pch(nd)
the size of the one-dimensional (helix) output data space.
Every filter output point is to be assigned to a patch.
All filters of a given patch number will be the same filter.
Nonstationary helixes are created with
createnhelixmod, which is a simple modification of module
createhelixmod ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
createnhelixmodcreate non-stationary helix
Notice that the user must define the pch(product(nd))
vector before creating a nonstationary helix.
For a simple 1-D time-variable filter,
presumably pch would be something like
.
createnhelixmodcreate non-stationary helix
Notice that the user must define the pch(product(nd))
vector before creating a nonstationary helix.
For a simple 1-D time-variable filter,
presumably pch would be something like
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)