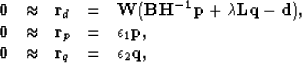
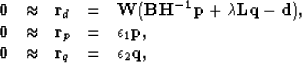 |
(26) |
| (27) |
 |
It is a customary matter of practice to forget the two ![]() s
and play with the
s
and play with the ![]() .If we kept the two
.If we kept the two ![]() s,
the choice of
s,
the choice of ![]() would be irrelevant to the final result.
Since we are going to truncate the iteration,
choice of
would be irrelevant to the final result.
Since we are going to truncate the iteration,
choice of ![]() matters.
It chooses how much data energy goes into the equipment drift function
and how much into topography.
Antoine ended out with with
matters.
It chooses how much data energy goes into the equipment drift function
and how much into topography.
Antoine ended out with with ![]() .
.
There is another parameter to adjust.
The parameter ![]() controlling the decay of the leaky integration.
Antoine found that value
controlling the decay of the leaky integration.
Antoine found that value ![]() was a suitable compromise.
Taking
was a suitable compromise.
Taking ![]() smaller allows the track drift to vary too rapidly thus
falsifying data in a way that falsifies topography.
Taking
smaller allows the track drift to vary too rapidly thus
falsifying data in a way that falsifies topography.
Taking ![]() closer to unity does not allow adequately rapid variation
of the data acquistion system
thereby pushing acquisition tracks into the topography.
closer to unity does not allow adequately rapid variation
of the data acquistion system
thereby pushing acquisition tracks into the topography.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (bottom-left corner)
shows the estimated roughened image
(bottom-left corner)
shows the estimated roughened image ![]() with
with ![]() data-drift modeling and
(top-left corner)
data-drift modeling and
(top-left corner) ![]() without it.
Data-drift modeling (bottom-left)
yields an image that is essentially track-free without loss of detail.
Top right shows the poor result of applying
the derivative
without it.
Data-drift modeling (bottom-left)
yields an image that is essentially track-free without loss of detail.
Top right shows the poor result of applying
the derivative ![]() along the tracks.
Tracks are removed but the topography is unclear.
along the tracks.
Tracks are removed but the topography is unclear.
The bottom-right part of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) provides important diagnostic information.
The estimated instrumentation drift
provides important diagnostic information.
The estimated instrumentation drift ![]() has been transformed
to model space
has been transformed
to model space ![]() .We do not like to see hints of geology in this space but we do.
Adjusting
.We do not like to see hints of geology in this space but we do.
Adjusting ![]() or
or ![]() we can get rid of the geology here,
but then survey tracks will appear in the lake image.
The issue of decomposing data into signal and noise parts
is dealt with further in chapter
we can get rid of the geology here,
but then survey tracks will appear in the lake image.
The issue of decomposing data into signal and noise parts
is dealt with further in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show
selected segments of data space.
Examining here the discrepancy between observed data and modeled data
offers us an opportunity to get new ideas.
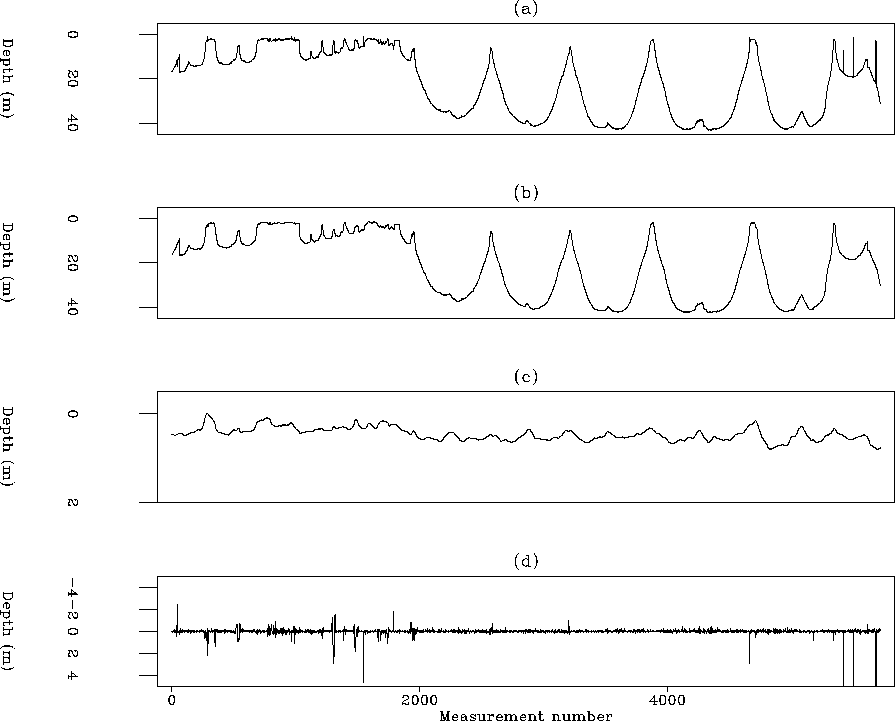
The top plot is the input data
show
selected segments of data space.
Examining here the discrepancy between observed data and modeled data
offers us an opportunity to get new ideas.
The top plot is the input data ![]() .Next is the estimated noise-free data
.Next is the estimated noise-free data ![]() .Then the estimated secular variations
.Then the estimated secular variations ![]() .Finally residual
.Finally residual
![]() after a suitable number of iterations.
The modeled data in both Figures
after a suitable number of iterations.
The modeled data in both Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b and
b and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b show no remaining spikes.
b show no remaining spikes.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
(b) The estimated noise-free data
.
(b) The estimated noise-free data  |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
(b) Modeled data,
.
(b) Modeled data,
The estimated instrument drift is reasonable, mostly under a meter
for measurments with a nominal precision of 10 cm.
There are some obvious problems though.
It is not a serious problem that the drift signal is always positive.
Applying the track derivative means that zero frequency is in the null space.
An arbitrary constant may be moved
from water depth to track calibration.
More seriously, the track calibration fluctuates
more rapidly than we might imagine.
Worse still, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c shows
the instrument drift correlates with water depth(!).
This suggests we should have a slower drift function
(bigger
c shows
the instrument drift correlates with water depth(!).
This suggests we should have a slower drift function
(bigger ![]() or weaker
or weaker ![]() ), but Antoine assures me that
this would push data acquisition tracks into the lake image.
If the data set had included the date-time of each measurement
we would have been better able to model drift.
Instead of allowing a certain small change of drift with each measurement,
we could have allowed a small change
in proportion to the time since the previous measurement.
), but Antoine assures me that
this would push data acquisition tracks into the lake image.
If the data set had included the date-time of each measurement
we would have been better able to model drift.
Instead of allowing a certain small change of drift with each measurement,
we could have allowed a small change
in proportion to the time since the previous measurement.
An interesting feature of the data residual in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d is
that it has more variance in deep water than in shallow.
Perhaps the depth sounder has insufficient power for deeper water
or for the softer sediments found in deeper water.
On the other hand, this enhanced deep water variance
is not seen in Figure
d is
that it has more variance in deep water than in shallow.
Perhaps the depth sounder has insufficient power for deeper water
or for the softer sediments found in deeper water.
On the other hand, this enhanced deep water variance
is not seen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d which is puzzling.
Perhaps the sea was rough for one day of recording but not another.
d which is puzzling.
Perhaps the sea was rough for one day of recording but not another.