




Next: Preconditioning for accelerated convergence
Up: ELIMINATING NOISE AND SHIP
Previous: ELIMINATING NOISE AND SHIP
Let 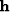 be an abstract vector containing as components
the water depth over a 2-D spatial mesh.
Let
be an abstract vector containing as components
the water depth over a 2-D spatial mesh.
Let 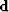 be an abstract vector whose successive components
are depths along the vessel tracks.
One way to grid irregular data is to minimize the length
of the residual vector
be an abstract vector whose successive components
are depths along the vessel tracks.
One way to grid irregular data is to minimize the length
of the residual vector 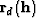 :
:
| 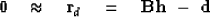 |
(20) |
where 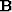 is a 2-D linear interpolation (or binning) operator
and
is a 2-D linear interpolation (or binning) operator
and 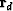 is the data residual.
Where tracks cross or where multiple data values end up in the same bin,
the fitting goal (20) takes an average.
Figure
is the data residual.
Where tracks cross or where multiple data values end up in the same bin,
the fitting goal (20) takes an average.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a display of simple binning of the raw data.
(Some data points are outside the lake.
These must represent navigation errors.)
is a display of simple binning of the raw data.
(Some data points are outside the lake.
These must represent navigation errors.)
Some model-space bins will be empty.
For them we need an additional ``model styling'' goal,
i.e. regularization.
For simplicity we might minimize the gradient.
| 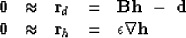 |
(21) |
where 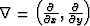 and
and 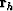 is the model space
residual.
Choosing a large scaling factor
is the model space
residual.
Choosing a large scaling factor  will tend to smooth
our entire image, not just the areas of empty bins.
We would like
will tend to smooth
our entire image, not just the areas of empty bins.
We would like  to be any number small enough
that its main effect is to smooth areas of empty bins.
When we get into this further, though, we'll see that
because of noise
some smoothing across the nonempty bins is desireable too.
to be any number small enough
that its main effect is to smooth areas of empty bins.
When we get into this further, though, we'll see that
because of noise
some smoothing across the nonempty bins is desireable too.





Next: Preconditioning for accelerated convergence
Up: ELIMINATING NOISE AND SHIP
Previous: ELIMINATING NOISE AND SHIP
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a display of simple binning of the raw data.
(Some data points are outside the lake.
These must represent navigation errors.)
is a display of simple binning of the raw data.
(Some data points are outside the lake.
These must represent navigation errors.)