




Next: Seabeam: theory to practice
Up: LEVELED INVERSE INTERPOLATION
Previous: Test results for leveled
Here we see how the interpolation beyond aliasing was done.
interpolation ! beyond aliasing
The first ``statement of wishes'' is that the observational data 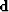 should result from a linear interpolation
should result from a linear interpolation 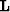 of the uniformly sampled
model space
of the uniformly sampled
model space 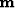 ; that is,
; that is,
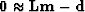 .Expressing this as a change
.Expressing this as a change 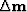 gives the fitting goal
in terms of the model change,
gives the fitting goal
in terms of the model change,
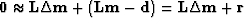 .The second wish is really an assertion
that a good way to find missing parts of a function
(the model space)
is to solve for the function and its PEF at the same time.
We are merging the fitting goal
(
.The second wish is really an assertion
that a good way to find missing parts of a function
(the model space)
is to solve for the function and its PEF at the same time.
We are merging the fitting goal
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for irregularly sampled data with the fitting goal
(42) for finding the prediction-error filter.
) for irregularly sampled data with the fitting goal
(42) for finding the prediction-error filter.
| 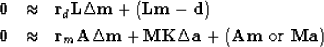 |
(48) |
| (49) |
Writing this out in full for 3 data points
and 6 model values on a uniform mesh
and a PEF of 3 terms,
we have
| ![\begin{displaymath}
\left[
\begin{array}
{cccccc\vert ccc}
.8 & .2 & . & . & ....
...r_{m6} \\ r_{m7}
\end{array} \right]
\quad \approx \ \bold 0\end{displaymath}](img123.gif) |
(50) |
where rm is the convolution of the filter at and the model mt,
where rd is the data misfit 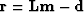 ,and where
,and where 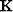 was defined in equation (11).
fitting goal ! nonlinear
was defined in equation (11).
fitting goal ! nonlinear
Before you begin to use this nonlinear fitting goal,
you need some starting guesses for 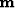 and
and  .The guess
.The guess 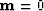 is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
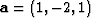 as I did for the examples here.
as I did for the examples here.





Next: Seabeam: theory to practice
Up: LEVELED INVERSE INTERPOLATION
Previous: Test results for leveled
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for irregularly sampled data with the fitting goal
(42) for finding the prediction-error filter.
) for irregularly sampled data with the fitting goal
(42) for finding the prediction-error filter.
![\begin{displaymath}
\left[
\begin{array}
{cccccc\vert ccc}
.8 & .2 & . & . & ....
...r_{m6} \\ r_{m7}
\end{array} \right]
\quad \approx \ \bold 0\end{displaymath}](img123.gif)
![]() and
and ![]() .The guess
.The guess ![]() is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
is satisfactory (as explained later).
For the first guess of the filter, I suggest you load it up with
![]() as I did for the examples here.
as I did for the examples here.