




Next: Differentiation by a complex
Up: MULTIVARIATE LEAST SQUARES
Previous: Inside an abstract vector
An important concept is that when energy is minimum,
the residual is orthogonal to the fitting functions.
The fitting functions are the column vectors
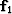 ,
, 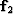 , and
, and 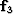 .Let us verify only that the dot product
.Let us verify only that the dot product 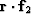 vanishes;
to do this, we'll show
that those two vectors are orthogonal.
Energy minimum is found by
vanishes;
to do this, we'll show
that those two vectors are orthogonal.
Energy minimum is found by
| 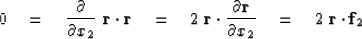 |
(31) |
(To compute the derivative refer to equation (13).)
Equation (31) shows that
the residual is orthogonal to a fitting function.
The fitting functions are the column vectors in the fitting matrix.
The basic least-squares equations are often called
the ``normal" equations.
The word ``normal" means perpendicular.
We can rewrite equation
(28)
to emphasize the perpendicularity.
Bring both terms to the left,
and recall the definition of the residual  from equation (13):
from equation (13):
| 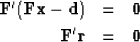 |
(32) |
| (33) |
Equation (33) says that the residual vector  is perpendicular to
each row in the
is perpendicular to
each row in the 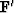 matrix.
These rows are the fitting functions.
Therefore, the residual, after it has been minimized,
is perpendicular to
all
the fitting functions.
matrix.
These rows are the fitting functions.
Therefore, the residual, after it has been minimized,
is perpendicular to
all
the fitting functions.





Next: Differentiation by a complex
Up: MULTIVARIATE LEAST SQUARES
Previous: Inside an abstract vector
Stanford Exploration Project
4/27/2004
![]() ,
, ![]() , and
, and ![]() .Let us verify only that the dot product
.Let us verify only that the dot product ![]() vanishes;
to do this, we'll show
that those two vectors are orthogonal.
Energy minimum is found by
vanishes;
to do this, we'll show
that those two vectors are orthogonal.
Energy minimum is found by
![]() from equation (13):
from equation (13):