![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
we have the operator in (16).
,
we have the operator in (16).
The linear interpolation
operator is much like the binning operator but a little fancier.
When we perform the forward operation, we take each data coordinate
and see which two model bin centers bracket it.
Then we pick up the two bracketing model values
and weight each of them
in proportion to their nearness to the data coordinate,
and add them to get the data value (ordinate).
The adjoint operation is adding a data value
back into the model vector;
using the same two weights,
the adjoint distributes the data ordinate value
between the two nearest bins in the model vector.
For example, suppose we have a data point near each end of the model
and a third data point exactly in the middle.
Then for a model space 6 points long,
as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
we have the operator in (16).
,
we have the operator in (16).
|
helgerud
Figure 4 Uniformly sampled model space and irregularly sampled data space corresponding to (16). | 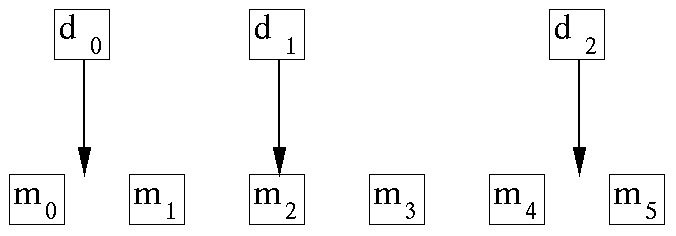 |
![\begin{displaymath}
\left[
\begin{array}
{c}
d_0 \\
d_1 \\
d_2
\end{ar...
...m_1 \\
m_2 \\
m_3 \\
m_4 \\
m_5
\end{array}\right]\end{displaymath}](img52.gif) |
(16) |
Module lint1 does linear interpolation and its adjoint.
In chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we build inverse operators.
lint1linear interp
we build inverse operators.
lint1linear interp