GETTING THE WAVES FROM THE REFLECTION COEFFICIENTS

A layered material may be specified by giving the reflection coefficient at each interface. Alternate descriptions are to give any one of the scattered waves R(Z), E(Z), X(Z), or P(Z). Our ultimate objective is to get such a good grip on the algebra of this kind of problem that we will be able to start with any descriptor of the layers and from it deduce all the other descriptors.

An important result of the last section was the development of a ``layer matrix" (14) that is, a matrix which can be used to extrapolate waves observed in one layer to the waves observed in the next layer. This process may be continued indefinitely. To see how to extrapolate from layer 1 to layer 3 substitute (14) with k = 1 into (14) with k = 2, obtaining

$$\begin{eqnarray} \left[ \begin{array} {c} U \\ D \end{array} \right] _3 & = &... ...ight] \; \left[ \begin{array} {c} U \\ D \end{array} \right] _1\end{eqnarray}$$ (24)

Inspection of this example suggests the general form for a product of k layer matrices  

$${1 \over \sqrt{Z}^k \prod^k_{j=1}\,t_j} \; \left[ \begin{ar... ...t] G(Z) & Z^k F \left( {1 \over Z} \right) \end{array} \right]$$ (25)

Now let us verify that (25) is indeed the general form. We assume (25) is correct for k - 1; then we multiply (25) by another layer matrix and see if the product retains the same form with k - 1 increased to k. The product is

$$\begin{eqnarray} {1 \over \sqrt{Z}t_k} \; \left[ \begin{array} {lc} 1 & c_kZ \... ...Z} \right) + Z^k F \left( {1 \over Z} \right) \end{array} \right]\end{eqnarray}$$ (26)

By inspecting the product we see that the scaling factor is of the same form with k - 1 changed to k. Also the 22 matrix element can be obtained from the 11 element by replacing Z with 1/Z and multiplying by Z^k. Likewise, the 21 element is obtained from the 12 element; thus (25) does indeed represent a general form. The polynomials F(Z) and G(Z) of order k are built up, starting from F₁=1 and G₁=c₁, in the following way [from the first column of the right-hand side of (26)]:

$$\begin{eqnarray} F_k(Z) &=& F_{k-1}(Z) + c_kZG_{k-1}(Z) \\ G_k(Z) &=& c_k \, F_{k-1}(Z) + ZG_{k-1}(Z)\end{eqnarray}$$ (27) (28)

By inspecting (27) and (28) we can see some of the details of F and G. From (27) we see that the lead coefficient f₀ of F(Z) does not change with k. It is always (f₀)_k = 1. Knowing this from (28) we see that (g₀)_k = c_k. Also with knowledge that F(Z) and G(Z) are of the same degree in Z, we see that (28) implies that the highest coefficient of G(Z), say (g_k)_k does not change with k and therefore it equals the starting value of c₁. Finally, with this knowledge and (27) we deduce that the highest coefficient in F(Z) will always be c₁ c_k. Thus, for k>1

$$\begin{eqnarray} F_k(Z) &= &1 + f_1Z + f_2Z^2 + \cdots + c_1 c_k Z^{k - 1} \\ G_k(Z) &= & c_k + g_1Z + g_2Z^2 + \cdots + c_1Z^{k - 1}\end{eqnarray}$$ (29) (30)

It may be noted in (29) and (30) and proved from the recurrence relations (27) and (28) that the coefficients of F contain even powers of c and that G contains odd powers of c. This means that if all c change sign, G will change sign but F is unchanged.

The polynomials F(Z) and G(Z) are not independent and a surprising energy-flux-like relationship exists between them. By substitution from (27) and (28) one may directly verify that  

$$\left[ F(Z)F \left( {1 \over Z} \right) - G(Z)G \left( {1 ... ...r Z} \right) - G(Z)G \left( {1 \over Z} \right) \right] _{k-1}$$ (31)

Since F₁(Z) = 1 and G₁(Z) = c₁ we have by iterative application of (31) that  

$$\left[ F(Z)F \left( {1 \over Z} \right) - G(Z)G \left( {1 \... ...\right]_k \eq \prod^{k}_{1} (1 - {c_k}^2) \eq \prod^{k}_{1} t't$$ (32)

Equation (32) is a surprising equation because on the left-hand side we have two spectra, the spectrum of f_t and the spectrum of g_t, but the right-hand side is a positive, frequency-independent constant. Since the spectrum of f_t is thus greater than the spectrum of g_t, we may apply the theorem of adding garbage to a minimum-phase wavelet to deduce from (27) and from knowledge that |c_k| < 1 that F_k(Z) is minimum-phase if F_k-1(Z) is minimum-phase. Since F₁(Z) = 1 is minimum-phase, we see that all F_k(Z) are minimum-phase. Since F(Z) is minimum-phase, then F(Z) may be calculated from its spectrum F(Z)F(1/Z) or the spectrum of g_t (along with the single number $\Pi t't$). However, we cannot get G from F. Before continuing our algebraic discussion we take up an example.

Let a stack of layers be sandwiched in between two halfspaces Figure 9. An impulse is incident from below. The backscattered wave is called C(Z) and the transmitted wave is called T(Z).

 

8-9
Figure 11 Waves incident, reflected, and transmitted from a stack of layers between two half-spaces.

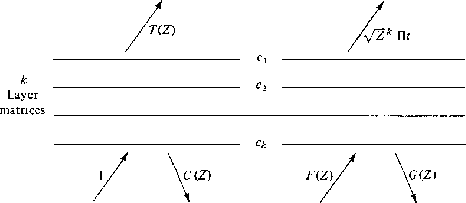Mathematically, we describe the situation with the equations  

$$\left[ \begin{array} {c} 1 \\ C(Z) \end{array} \right] \e... ...t] \; \left[ \begin{array} {c} T(Z) \\ 0 \end{array} \right]$$ (33)

We may solve the first of (33) for the transmitted wave T(Z)  

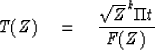$$T(Z) \eq {\sqrt{Z}^k \Pi t \over F(Z)}$$ (34)

and introduce the result back into the second of (33) to obtain the backscattered wave  

$$C(Z) \eq {G(Z)T(Z) \over \sqrt{Z}^k \Pi t} \eq {G(Z) \over F(Z)}$$ (35)

The mathematical fact that F(Z) is minimum-phase corresponds to the physical fact that the C(Z) and T(Z) have finite energy; therefore the denominators of (34) and (35) cannot have zeros inside the unit circle. Since we know that the backscattered wave C(Z) contains less energy than the incident wave by reference to (23) we know that a positive real function is given by  

$${1 - C(Z) \over 1 + C(Z)} \eq {1 - G(Z)/F(Z) \over 1 + G(Z)/F(Z)}$$ (36)

Now let us see how to reconstruct the reflection coefficients c_j from the observed scattered wave C(Z). Referring to Figure 9 we have  

$$\left[ \begin{array} {c} 1 \\ C(Z) \end{array} \right] \e... ...t] \; \left[ \begin{array} {c} U \\ D \end{array} \right] _k$$ (37)

The first coefficient of C(Z) is c_k [this is physically obvious but may also be seen from (30)]. Thus the layer matrix in (37) is known. Multiplying (37) through by the inverse of the layer matrix we will have obtained U_k-1(Z) and D_k-1(Z). The next reflection coefficient c_k-1 is obviously d₀/u₀. Thus we may proceed until all the c_k are determined.

Next let us reconsider the reflection seismology geometry. We have  

$$\left[ \begin{array} {c} 0 \\ E(Z) \end{array} \right] \e... ... \; \left[ \begin{array} {c} -R \\ 1 + R \end{array} \right]$$ (38)

From the first equation we may solve for R(Z)  

$$R(Z) \eq + {Z^k G(1/Z) \over F(Z) - Z^k G(1/Z)}$$ (39)

The denominator occurs so often that we give it the name A(Z)  

$$A_k(Z) \eq F_k(Z) - Z^k G_k \left( {1 \over Z} \right)$$ (40)

A(Z), like F(Z), is minimum-phase. The second of (38) gives the escaping wave as

simplifying with (32) we get  

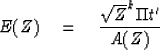$$E(Z) \eq {\sqrt{Z}^k \Pi t' \over A(Z)}$$ (41)

Let us confirm that the definition (40) of A_k(Z) is consistent with our chapter definition of the Levinson recursion (). First, rewrite (40) in various ways

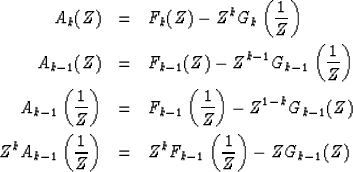$$\begin{eqnarray} A_k(Z) &=& F_k(Z) - Z^k G_k \left( {1 \over Z} \right)\quad\\ A... ...ght)&=& Z^k F_{k-1}\left( {1 \over Z} \right)- Z G_{k-1} (Z) \quad\end{eqnarray}$$ (42) (43) (44) (45)

Now insert the recurrence relations (27) and (28) into the definition (42) getting

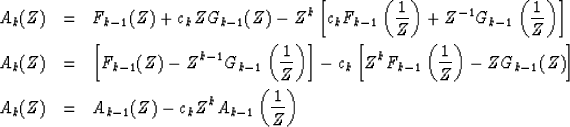$$\begin{eqnarray} A_k(Z)&=& F_{k-1}(Z)+c_kZG_{k-1}(Z) - Z^k \left[ c_kF_{k-1}\le... ... A_k(Z)&=& A_{k-1}(Z) - c_k Z^k A_{k-1} \left( {1 \over Z} \right)\end{eqnarray}$$ (46) (47) (48)

which is the Levinson recursion as asserted. The recursion begins from A₀=1.

The positive real function is

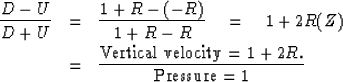$$\begin{eqnarray} {D - U \over D + U} & = & {1 + R - (-R) \over 1 + R - R} \eq 1 ... ...{Vertical velocity} = 1 + 2R. \over \mbox{Pressure} = 1} \nonumber\end{eqnarray}$$ (49)

As mentioned earlier, if the equations are interpreted in terms of acoustics, then Y(D - U)/(D + U) is interpreted as vertical velocity divided by pressure. It is called the admittance which is the inverse of the impedance.

We have now completed the task of solving for the waves given the reflection coefficients. In the subsequent section we attach the inverse problems of getting the reflection coefficients from knowledge of various waves.

EXERCISES:

1. In Figure 9 let $c_1 = {1 \over 2}$, $c_2 = -{1 \over 2}$,and $c_3 = {1 \over 3}$.What are the polynomial ratios T(Z) and C(Z)?
2. For a simple interface, we had the simple relations t = 1 + c, t' = 1 + c', and c = -c'. What sort of analogous relations can you find for the generalized interface of Figure 9? [For example, show 1 - T(Z)T'(1/Z) = C(Z)C(1/Z) which is analogous to 1 - tt' = c².]
3. Show that T(Z) and T'(Z) are the same waveforms within a scale factor. Deduce that many different stacks of layers may have the same T(Z).
4. Let an impulse be incident on a stack of layers and let a wave C(Z) be reflected. What is the reflection coefficient at the first layer encountered? What would be the reflected wave as a function of C for a situation which differs from the above by the removal of the first reflector?
5. Consider the earth to be modeled by layers over a halfspace. Let an impulse be incident from below (Figure 10). Given F(Z) and G(Z), elements of the product of the layer matrices, solve for X and for P. Check your answer by showing that $P(Z) \bar{P}(1/Z) = 1$.How is X related to E? This relation illustrates the principle of reciprocity which says source and receiver may be interchanged.
    

   E8-3-5 Figure 9 Earthquake geometry.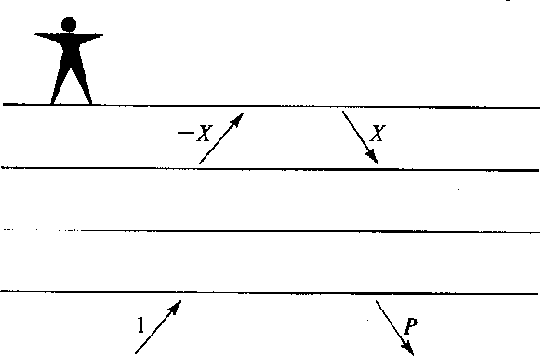

   

6. Show that $1 + R(1/Z) + R(Z) = (\mbox{scale factor}) X(Z) X(1/Z)$,which shows that one may autocorrelate the transmission seismogram to get the reflection seismogram.
7. Refer to Figure 11. Calculate R' from R.
    

   E8-3-7 Figure 10 Stripping off the surface layer.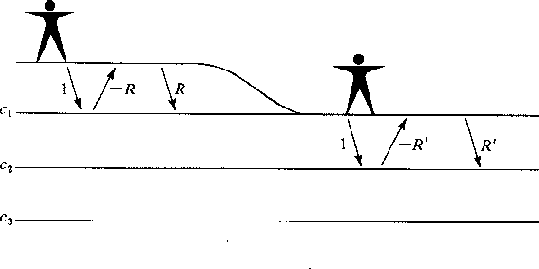