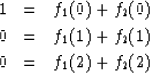
A common geophysical situation is a plane wave (signal) incident on a group of receivers. One expects to see the same waveform at each receiver. However, there is corrupting noise present at each receiver, and the noise may or may not be coherent from one receiver to the next. In fact, we may suppose there is so much noise on each receiver that the signal might not be detectable at all if there were only one receiver. This was the situation facing M.J. Levin when he was trying to detect weak underground nuclear explosions with an array of seismometers. He suggested a multichannel filter with constraints. First suppose that either all the signals arrive at the same time or that, if the times differ, at least they are known so that the data channels may be shifted into alignment. Now the problem is to filter each channel and then add up the channels; the noise should be rejected but the signal shape should be maintained. Let fi(j) represent the filter weight on the ith channel at the jth lag. For illustration, consider two channels and three lag times. Then Levin's constraints which prevent signal distortion are
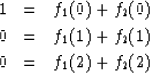 |
||
| (40) | ||
That this does not cause signal distortion follows, since if the same signal s(Z) comes into each channel, the output is merely s(Z)[f1(Z) + f2(Z)]. But f1 + f2 is just (1, 0, 0) in this case or a delta function in general. We call the equation set (40) constraint equations because there are fewer equations than unknowns. The constraint equations may be written in usual form as
![\begin{displaymath}
\left[
\begin{array}
{rllllll}
-1 & 1 & 1 & 0 & 0 & 0 & 0 \...
...\eq \left[
\begin{array}
{c}
0 \\ 0 \\ 0 \end{array} \right]\end{displaymath}](img90.gif) |
(41) |
which may abbreviate as Gf = 0. If we use the method of least squares to minimize the total energy in the filter output, we will be attempting to suppress both signal and noise. But the constraint equations prevent the suppression of signal; hence only the noise is attenuated. If we let R denote the spectral matrix of the input data, then the filter f is determined by solving equations like
![\begin{displaymath}
\left[
\begin{array}
{ll}
{\bf R}& {\bf G}^T \\ \ & \ \\ ...
...left[
\begin{array}
{c}
V \\ 0 \\ \vdots \end{array} \right]\end{displaymath}](img91.gif) |
(42) |