Next: DESIGN OF MULTICHANNEL FILTERS
Up: Waveform applications of least
Previous: BURG SPECTRAL ESTIMATION
An adaptive filter is one which changes
with time to accommodate itself to changes in the
time series being filtered.
For example,
suppose one were predicting one point
ahead in a time series.
One could take a lot of past data to design the filter;
then one could apply the filter to present incoming
data to predict future incoming data.
Below is a
computer program to do the Burg algorithm.
The program follows the notation of the text.
The data X is a vector of dimension given to be LX.
Choice of 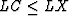 is a compromise between high resolution
and high scatter. The density of points on the frequency axis,
which is controlled by
is a compromise between high resolution
and high scatter. The density of points on the frequency axis,
which is controlled by 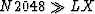 , is chosen for plotting
convenience and should be great enough to resolve narrow
spectral lines.
, is chosen for plotting
convenience and should be great enough to resolve narrow
spectral lines.
SUBROUTINE BURGC (LX,X,EP,EM,LC,C,A,N2048,S)
C GIVEN A TIME SERIES X(1...LX) GET ITS LOG SPECTRUM S(1...N2048)
DIMENSION X(LX),EP(LX),EM(LX),C(LC),A(LC),S(N2048)
COMPLEX X,EP,EM,C,A,S,TOP,BOT,EPI,CONJG,CLOG
DO 10 I=1,N2048
10 S(I)=O.
A(1)=1.
DO 20 I=1,LX
EM(I)=X(I)
20 EP(I)=X(I)
DO 60 J=2,LC
TOP=0.
BOT=0.
DO 30 I=J,LX
BOT=BOT+EP(I)*CONJG(EP(I))+EM(I-J+1)*CONJG(EM(I-J+1))
30 TOP=TOP+EP(I)*CONJG(EM(I-J+1))
C(J)=2*TOP/BOT
DO 40 I=J,LX
EPI=EP(I)
EP(I)=EP(I)-C(J)*EM(I-J+1)
40 EM(I-J+1)=EM(I-J+1)-CONJG(C(J))*EPI
A(J)=0.
DO 50 I=1,J
50 S(I)=A(I)-C(J)*CONJG(A(J-I+1))
DO 60 I=1,J
60 A(I)=S(I)
CALL FORK(N2048,S,+1.)
DO 70 I=1,N2048
70 S(I)=-CLOG(S(I))*2.
RETURN
END
As time goes on it might become desirable to
recompute the filter on the basis of new data which have come in.
How often should the filter be redesigned?
In concept,
there is no reason why it should not be recomputed very often,
perhaps after each new data point arrives.
In practice,
this is usually prohibitively expensive.
For a filter of length n it requires n multiplies
and adds to apply the filter to get one new output point.
To recompute the filter with Levinson recursion
requires about n2 multiply-adds.
However, it is usually expected that the filter need
only be changed by a very small amount when a new data
point arrives.
For that reason we will give the Widrow
adaptive-filter algorithm which modifies the filter by
means of only n arithmetic operations.
Thus, a new filter is computed after each data point
comes in.
For definiteness,
consider a two-term prediction situation
where et is the error in predicting a time series
xt from two of its past values
| 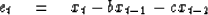 |
(19) |
The sum squared error in the prediction is
| 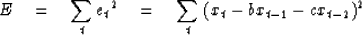 |
(20) |
If the parameter b has been chosen correctly,
one should find that 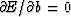 .However,
if the nature of the time series xt is changing with time,
.However,
if the nature of the time series xt is changing with time,
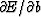 may depart from zero when
new data are included in the sum in (20).
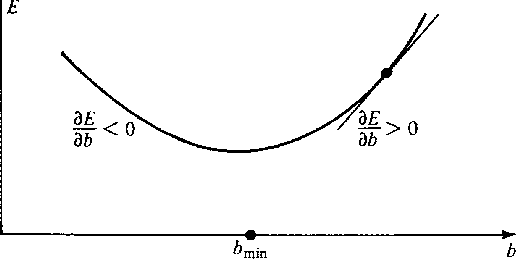
Since E is a positive quadratic function of b,
if
may depart from zero when
new data are included in the sum in (20).
Since E is a positive quadratic function of b,
if 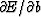 has become positive,
then b should be reduced.
If
has become positive,
then b should be reduced.
If 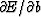 has become negative,
then b should be augmented. See Figure 1.
has become negative,
then b should be augmented. See Figure 1.

From (20) we have
| 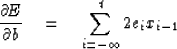 |
(21) |
The change in 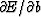 from the addition
of the data point xt is just
-2etxt-1; thus,
we are motivated to modify b and c in the following way
from the addition
of the data point xt is just
-2etxt-1; thus,
we are motivated to modify b and c in the following way
| ![\begin{displaymath}
\left[
\begin{array}
{c}
b \\ c \end{array} \right]
\lefta...
...eft[
\begin{array}
{l}
x_{t-1} \\ x_{t-2} \end{array} \right]\end{displaymath}](img54.gif) |
(22) |
Here the number k scales the amount of the
readjustment which we are willing to make to
b and c in one time step.
If k is chosen very small,
the adjustment will take place very slowly.
If k is chosen too large, the adjustment will
overshoot the minimum;
however one may hope that it will bounce back,
perhaps again overshooting at the next step.
The choice of k is dictated in part by the
nature of the time series xt under study.
There are many variations on these same ideas.
For example,
we could use the L1 norm and minimize something like
| 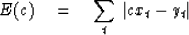 |
(23) |
The resulting adaptation would be
| 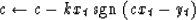 |
(24) |
Equation (23) is of course the weighted median.
An even more robust procedure is the uniformly weighted median
| 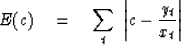 |
(25) |
which leads to the adaptation
| 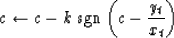 |
(26) |
which is identical to
| 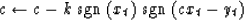 |
(27) |
The examples (23) and (25) could be extended,
in a manner like the Burg algorithm,
to stationary series.
Like (25) we could minimize
| 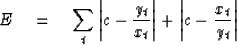 |
(28) |
This leads to a choice of c within the proper bounds because
EXERCISES:
- If xt has physical dimensions of volts,
what should be the physical dimensions for k?
If xt has an rms value of 100 V and
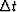 ,the sampling interval, is 1 ms,
what numerical value of k will allow the Widrow filter
to adapt to new conditions in about a second?
,the sampling interval, is 1 ms,
what numerical value of k will allow the Widrow filter
to adapt to new conditions in about a second?
- Consider the time series
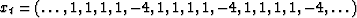 .Consider self-prediction of the form xt+1 = cxt.
What are the results of least-squares prediction?
What are the results of L1 norm prediction of data
weighted and uniformly weighted types?
.Consider self-prediction of the form xt+1 = cxt.
What are the results of least-squares prediction?
What are the results of L1 norm prediction of data
weighted and uniformly weighted types?





Next: DESIGN OF MULTICHANNEL FILTERS
Up: Waveform applications of least
Previous: BURG SPECTRAL ESTIMATION
Stanford Exploration Project
10/30/1997