HOUSEHOLDER TRANSFORMATIONS AND GOLUB'S METHOD

Our previous discussions of least squares always led us to matrices of the form ${\bf A}^T {\bf A}$which then needed to be inverted. Golub's method of using Householder transformations works directly with the matrix ${\bf A}$ and has the advantage that it is considerably more accurate than methods with invert ${\bf A}^T {\bf A}$.It seems that about twice as much precision is required to invert ${\bf A}^T {\bf A}$ than is needed to deal directly with ${\bf A}$.Another reason for learning about Golub's method is that the calculation is organized in a completely different way; therefore, it will often turn out to have other advantages or disadvantages which differ from one application to the next.

A reflection transformation is a matrix of the form ${\bf R}= ({\bf I}- 2{\bf v}{\bf v}^T /{\bf v}^T{\bf v})$ where ${\bf v}$ is an arbitrary vector. Obviously ${\bf R}$ is symmetric, that is, ${\bf R}= {\bf R}^T$.It also turns out that the reflection transformation is its own inverse, that is, ${\bf R}= {\bf R}^{-1}$.To see this, we verify by substitution that ${\bf R}^2 - {\bf I}$.

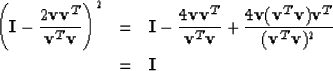$$\begin{eqnarray} \left( {\bf I}- {2{\bf v}{\bf v}^T \over {\bf v}^T {\bf v}} \ri... ...){\bf v}^T \over ({\bf v}^T {\bf v})^2} \\ & = & {\bf I}\nonumber \end{eqnarray}$$ (50)

A matrix transformation ${\bf M}$ is said to be unitary if ${\bf M}^T {\bf M}= {\bf I}$.When a matrix ${\bf M}$ is unitary it means that the vector ${\bf x}$ has the same length as the vector ${\bf M}{\bf x}$.These lengths are ${\bf x}^T{\bf x}$ and $({\bf M}{\bf x})^T({\bf M}{\bf x}) = {\bf x}^T{\bf M}^T{\bf M}{\bf x}= {\bf x}^T{\bf I}{\bf x}= {\bf x}^T{\bf x}$ which are the same. Reflection transformations are unitary because ${\bf R}^{-1} = {\bf R}^T$.They have a simple physical interpretation. Consider an orthogonal coordinate system in which one of the coordinate axes is aligned along the ${\bf v}$ vector. Reflection transformation reverses the sign of this coordinate axis vector (since ${\bf R}{\bf v}= -{\bf v}$) but it leaves unchanged all the other coordinate axis vectors. Thus it is obvious geometrically that reflection transformations preserve lengths and that applying the transformation twice returns any original vector to itself. Now, we seek a special reflection transformation called the Householder transformation which converts a matrix of the form on the left side to the form on the right where a is an arbitrary element  

$${\bf H}\left[ \begin{array} {cccc} a & a & a & a \\ 0 & a ... ...& a & a \\ 0 & 0 & 0 & a \\ 0 & 0 & 0 & a \end{array} \right]$$ (51)

Having determined the required transformation, we will know how to convert any matrix to an upper triangular form like  

$$\left[ \begin{array} {cccc} a & a & a & a \\ 0 & a & a & a... ...& 0 & a \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]$$ (52)

by a succession of Householder transforms. Golub recognized the value of this technique in solving overdetermined sets of simultaneous equations. He noted that when the error vector ${\bf e}= {\bf A}{\bf x}- {\bf b}$ is transformed by a unitary matrix ${\bf U}{\bf e}$ the problem of minimizing the length $({\bf e}^T{\bf U}^T{\bf U}{\bf e})^{1/2}$ of ${\bf U}{\bf e}$ by variation of ${\bf x}$ reduces to exactly the same problem as minimizing the length $({\bf e}^T{\bf e})^{1/2}$ of ${\bf e}$with respect to variation of ${\bf x}$.Thus a succession of Householder transforms could be found to reduce ${\bf e}= {\bf A}{\bf x}- {\bf b}$to the form  

$$\left[ \begin{array} {c} \\ {\bf e}_1 \\ \\ - \\ \\ {\... ... {c} a \\ a \\ a \\ a \\ a \\ a \\ a \end{array} \right]$$ (53)

Now for the clever observation that because of the zeros in the bottom part of the transformed ${\bf A}$ matrix there is no possibility of choosing any x_i values which alter ${\bf e}_2$ in any way. The top part of the transformed ${\bf A}$ matrix is an upper triangular matrix which for any value of ${\bf e}_1$can be solved exactly for the x_i. The least-squares solution x_i is the one for which ${\bf e}_1$ has been set equal to zero.

Now we turn to the task of finding the special reflection transformation, called the Householder transformation, which accomplishes (51). Observe that the left-hand operator below is a reflection transformation for any numerical choice of s.

$$\left\{ \left[ \begin{array} {ccccc} 1 & & & & \\ & 1 & & ... ...} {c} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \end{array} \right]$$

 

$$\qquad \quad \qquad \qquad \qquad \qquad \eq \left[ \begin{a... ...n{array} {c} a_1 \\ a_2 \\ s \\ 0 \\ 0 \end{array} \right]$$ (54)

Alternatively, if (54) is to be valid, then s must take a particular value such that  

$$1 \eq {2 \over (a_3 - s)^2 + {a_4}^2 + {a_5}^2} [0 \quad 0... ...y} {c} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \end{array} \right]$$ (55)

or  

$$1 \eq {-2sa_3 + 2({a_3}^2 + {a_4}^2 + {a_5}^2) \over s^2 - 2sa_3 + ({a_3}^2 + {a_4}^2 + {a_5}^2)}$$ (56)

This will be true only for s given by  

$$s \eq \pm ({a_3}^2 + {a_4}^2 + {a_5}^2)^{1/2}$$ (57)

Now let us see why the left-hand operator in (54) can achieve (51). Choice of the a vector as the third column in the matrix of (51) introduces the desired zeros on the right-hand side. Finally, it is necessary also to observe that this choice of ${\bf H}$ does not destroy any of the zeros which already existed on the left-hand side in (51).

A subroutine for least squares fitting programmed by Don C. Riley. (This program does not do the square matrix case. It is necessary that M > N.)

        SUBROUTINE GOLUB  (A,X,B,M,N)
C
C       A(M,N) ; B(M)   GIVEN WITH M>N    SOLVES FOR X(N) SUCH THAT
C                  ||  B - AX || = MINIMUM
C       METHOD OF G.GOLUB,  NUMERISCHE MATHEMATIK  7,206-216 (1965)
C
        IMPLICIT DOUBLE PRECISION (D)
        REAL A(M,N),X(N),B(M),U(50)
C.........DIMENSION U(M)
C.........PERFORM N ORTHOGONAL TRANSFORMATIONS TO A(.,.) TO
C.........UPPER TRIANGULARIZE THE MATRIX
        DO 3010 K=1,N
        DSUM=0.0D0
        DO 1010 I=K,M
        DAJ=A(I,K)
  1010  DSUM=DSUM+DAJ**2
        DAI=A(K,K)
        DSIGMA=DSIGN(DSQRT(DSUM),DAI)
        DBI=DSQRT(1,0D0+DAI/DSIGMA)
        DFACT=1.0D0/(DSIGMA*DBI)
        U(K)=DBI
        FACT-=DFACT
        KPLUS=K+1
        DO 1020 I=KPLUS,M
  1020	U(I)=FACT*A(I,K)
C.........I - UU' IS A SYMMETRIC, ORTHOGONAL MATRIX WHICH WHEN APPLIED
C......... TO A(.,.) WILL ANNIHILATE THE ELEMENTS BELOW THE DIAGONAL K
        DO 2030 J=K,N
c.........APPLY THE ORTHOGONAL TRANSFORMATION
        FACT=0.0
        DO 2010 I=K,M
  2010  FACT=FACT+U(I)*A(I,J)
        DO 2020 I=K,M
  2020	A(I,J)=A(I,J)-FACT*U(I)
  2030	CONTINUE
        FACT=0.0
        DO 2040 I=K,M
  2040	FACT=FACT+U(I)*B(I)
        DO 2050 I=K,M
  2050	B(I)=B(I)-FACT*U(I)
  3010	CONTINUE
C.........BACK SUBSTITUTE TO RECURSIVELY YIELD X(.)
        X(N)=B(N)/A(N,N)
        LIM=N-1
        DO 4020 I=1,LIM
        IROW=N-I			! error in first edition, was =N-1
        SUM=0.0
        DO 4010 J=1,I
  4010	SUM=SUM+X(N-J+1)*A(IROW,N-J+1)
  4020  X(IROW)=(B(IROW)-SUM)/A(IROW,IROW)
        RETURN
        END

Householder transformations can also be used in problems with constraints. In the set  

$$\left[ \begin{array} {c} {\bf C} \\ {\bf A}\end{array} \ri... ...left[ \begin{array} {c} {\bf d} \\ {\bf b}\end{array} \right]$$ (58)

one may desire to satisfy the top block exactly and the bottom block only in the least-squares sense. Define ${\bf y}$ as a succession of Householder transforms on ${\bf x}$;for example, ${\bf y} = {\bf H}_2{\bf H}_1{\bf x}$.Then substitute ${\bf x}= {\bf H}_1{\bf H}_2{\bf H}_2{\bf H}_1{\bf x}= {\bf H}_1{\bf H}_2{\bf y}$into (58). Householder transforms used as postmultipliers on the matrix of (58) can be chosen to introduce zeros in the top two rows of (58), for example  

$$\left[ \begin{array} {cccc} a & 0 & 0 & 0 \\ a & a & 0 & 0... ...y} {c} d_1 \\ d_2 \\ b_1 \\ b_2 \\ b_3 \end{array} \right]$$ (59)

Now we could use premultiplying Householder transforms on (59) to bring it to the form  

$$\left[ \begin{array} {cccc} a & 0 & 0 & 0 \\ a & a & 0 & 0... ...y} {c} d_1 \\ d_2 \\ b_1 \\ b_2 \\ b_3 \end{array} \right]$$ (60)

Since the top two equations of (59) or of (60) are to be satisfied exactly, then y₁ and y₂ are uniquely determined. They cannot be adjusted to help attain minimum error in the bottom three equations. Likewise the top two equations place no restraint on y₃ and y₄, so they may be adjusted to produce minimum error in the bottom three equations. No amount of adjustment in y₃ and y₄ can change the amount of error in the last equation, so we can ignore the last equation in the determination of y₃ and y₄. The third and fourth equations can be satisfied with zero error by suitable choice of y₃ and y₄. This must be the minimum-squared-error answer. Given ${\bf y}$ we can go back and get ${\bf x}$ with ${\bf x}= {\bf H}_1{\bf H}_2{\bf y}$.