




Next: FEWER EQUATIONS THAN UNKNOWNS
Up: Data modeling by least
Previous: MORE EQUATIONS THAN UNKNOWNS
It often happens that some observations are considered more reliable
than others. One may desire to weight the more reliable data more heavily
in the calculation. In other words, we may multiply the ith equation by a
weight 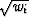
| ![\begin{displaymath}
\sqrt{w_i}
\; [-c_i\quad a_{i1} \quad a_{i2} \quad \cdots ]...
... \\
x_2 \\
\vdots \end{array} \right]
\eq \sqrt{w_i} e_i\end{displaymath}](img75.gif) |
(28) |
Now the weighted sum-squared error will be
| 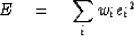 |
(29) |
Following the method of the last section,
it is easy to show that the x
which minimizes the weighted error E
of (29) is the x which
satisfies the simultaneous equations
| ![\begin{displaymath}
\left\{ \sum_{i} w_i
\; \left[
\begin{array}
{c}
-c_i \\ ...
...{array}
{c}
v \\
0 \\
0 \\
\vdots \end{array} \right]\end{displaymath}](img77.gif) |
(30) |
Choice of a set of weights
is often a rather subjective matter.
However,
if data are of uneven quality,
it cannot be avoided.
Omitting w is equivalent
to choosing it equal to unity.
A case of common interest
is where some equations should be solved exactly.
Such equations are called constraint equations.
Constraint equations often
arise out of theoretical considerations so they may,
in principle,
not have any error.
The rest of the equations often involve some measurement.
Since the measurement can often be made many times,
it is easy to get a lot more
equations than unknowns.
Since measurement always involves error,
we then use the method of least squares
to minimize the average error.
In order to be certain that the constraint equations are solved exactly,
one could use the trick of applying very large weight factors
to the constraint equations.
A problem is that
``very large'' is not well defined.
A weight equal 1010
might not be large enough
to guarantee the constraint equation is satisfied
with sufficient accuracy.
On the other hand, 1010 might lead to
disastrous round-off when solving
the simultaneous equations in a computer
with eight-digit accuracy.
The best approach is to analyze the situation
theoretically for 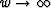 .
.
An example of a constraint equation
is that the sum of the xi equals M.
Another constraint would be x1 = x2.
Arranged in a matrix,
these two constraint equations are
| ![\begin{displaymath}
\left[
\begin{array}
{rcrccc}
-M & 1 & 1 & 1 & 1 & \cdots \...
...t]
\eq \left[
\begin{array}
{c}
0 \\
0 \end{array} \right]\end{displaymath}](img79.gif) |
(31) |
We write a general set of k constraint equations as
| ![\begin{displaymath}
{\bf G}
\left[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \\ ...
...eq \left[
\begin{array}
{c}
0 \\
\vdots \end{array} \right]\end{displaymath}](img80.gif) |
(32) |
Minimizing the error as 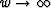 of the equations
is algebraically similar to
minimizing the error of Bx
of the equations
is algebraically similar to
minimizing the error of Bx 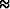 0.
The rows of
0.
The rows of 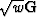 are just like some extra rows for B.
The resulting equation for x is
are just like some extra rows for B.
The resulting equation for x is
| ![\begin{displaymath}
\left\{ \sum^n_{i = 1}
\left[
\begin{array}
{c}
-c_i \\ ...
...
\begin{array}
{c}
v \\
0 \\
\vdots \end{array} \right]\end{displaymath}](img84.gif) |
(33) |
Now we will take all the wi
to equal 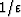 and we will let
and we will let  tend to zero. Also let
tend to zero. Also let
| 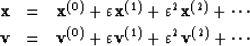 |
(34) |
| (35) |
With this, (33) may be written
| 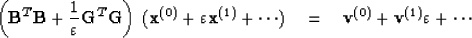 |
(36) |
Identify coefficients of powers of 
| 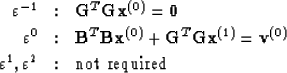 |
(37) |
| (38) |
| |
Equation (37) is m equations in m unknowns.
It will automatically be satisfied
if the k equations in (32) are satisfied.
Equation (38) appears to involve
the m unknowns in 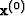 plus
m more unknowns in
plus
m more unknowns in 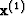 .
In fact,
we do not need
.
In fact,
we do not need 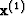 ;the k unknowns
;the k unknowns
|  |
(39) |
will suffice.
Arranging (38) and (32)
together and dropping superscripts,
we get a square matrix in m + k unknowns.
| ![\begin{displaymath}
\left[
\begin{array}
{c}
{\bf B}^T {\bf B} \\
\vbox{\h...
...t[
\begin{array}
{c}
v \\ 0 \\
\vdots \end{array} \right]\end{displaymath}](img93.gif) |
(40) |
Equation (40) is now a
simultaneous set for the unknowns  and
and 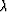 .
It might also be thought of as the solution to the problem
of minimizing the quadratic form
.
It might also be thought of as the solution to the problem
of minimizing the quadratic form
and since we can always transpose a scalar,
| 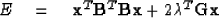 |
(41) |
According to the method of Lagrange multipliers,
one may minimize a quadratic
form subject to constraints by minimizing
instead a sum of the quadratic form
plus constraint terms where each constraint term
is the product of a constraint
equation multiplied by a
Lagrange multiplier 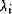 .
This is precisely
what we have in (41),
and the solution is given by
(40).
Lagrange multipliers frequently arise in connection with
integral equations.
The concept is readily transformed to matrices merely by
approximating integration by summation.
.
This is precisely
what we have in (41),
and the solution is given by
(40).
Lagrange multipliers frequently arise in connection with
integral equations.
The concept is readily transformed to matrices merely by
approximating integration by summation.
EXERCISES:
- In determining a density vs. depth profile
of the earth one might
minimize the squared difference between
some theoretical quantities (say, the frequencies of free oscillation)
and the observed quantities.
By astronomical means,
total mass and moment of inertia of the earth
are very well known.
If the earth is divided into
arbitrarily thin shells of equal thickness,
what are the two astronomical constraint equations
on the layer densities pi?
If the least-squares problem is nonlinear
(as it often is) it may be
linearized by assuming that
a given set of densities pi is a good guess
which satisfies the constraints and
doing least squares for the perturbation dpi.
What are the constraint equations on dpi?





Next: FEWER EQUATIONS THAN UNKNOWNS
Up: Data modeling by least
Previous: MORE EQUATIONS THAN UNKNOWNS
Stanford Exploration Project
10/30/1997
![]()
![\begin{displaymath}
\sqrt{w_i}
\; [-c_i\quad a_{i1} \quad a_{i2} \quad \cdots ]...
... \\
x_2 \\
\vdots \end{array} \right]
\eq \sqrt{w_i} e_i\end{displaymath}](img75.gif)
![\begin{displaymath}
\left\{ \sum_{i} w_i
\; \left[
\begin{array}
{c}
-c_i \\ ...
...{array}
{c}
v \\
0 \\
0 \\
\vdots \end{array} \right]\end{displaymath}](img77.gif)
![]() .
.![\begin{displaymath}
\left[
\begin{array}
{rcrccc}
-M & 1 & 1 & 1 & 1 & \cdots \...
...t]
\eq \left[
\begin{array}
{c}
0 \\
0 \end{array} \right]\end{displaymath}](img79.gif)
![\begin{displaymath}
{\bf G}
\left[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \\ ...
...eq \left[
\begin{array}
{c}
0 \\
\vdots \end{array} \right]\end{displaymath}](img80.gif)
![\begin{displaymath}
\left\{ \sum^n_{i = 1}
\left[
\begin{array}
{c}
-c_i \\ ...
...
\begin{array}
{c}
v \\
0 \\
\vdots \end{array} \right]\end{displaymath}](img84.gif)
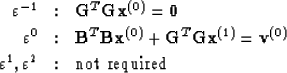
![\begin{displaymath}
\left[
\begin{array}
{c}
{\bf B}^T {\bf B} \\
\vbox{\h...
...t[
\begin{array}
{c}
v \\ 0 \\
\vdots \end{array} \right]\end{displaymath}](img93.gif)
![]() and
and ![]() .
It might also be thought of as the solution to the problem
of minimizing the quadratic form
.
It might also be thought of as the solution to the problem
of minimizing the quadratic form
![\begin{eqnarraystar}
E &= & [{\bf x}^T \quad \lambda^T]\left[
\begin{array}
{cc}...
... \lambda^T {\bf Gx} + {\bf x}^T {\bf G}^T
\lambda \nonumber \end{eqnarraystar}](img96.gif)
![]() .
This is precisely
what we have in (41),
and the solution is given by
(40).
Lagrange multipliers frequently arise in connection with
integral equations.
The concept is readily transformed to matrices merely by
approximating integration by summation.
.
This is precisely
what we have in (41),
and the solution is given by
(40).
Lagrange multipliers frequently arise in connection with
integral equations.
The concept is readily transformed to matrices merely by
approximating integration by summation.