




Next: CONFIDENCE INTERVALS
Up: Resolution
Previous: TIME-FREQUENCY-STATISTICAL RESOLUTION
The central-limit theorem of probability and statistics is perhaps the most
important theorem in the fields of probability and statistics.
A derivation of
the central limit theorem explains why the gaussian probability function is so
frequently encountered in nature;
not just in physics but also in the
biological and social sciences.
No experimental scientist should be unaware
of the basic ideas behind this theorem.
Although the result is very deep and
is even today the topic of active research,
we can get to the basic idea quite easily.
One way to obtain random integers from a known probability function is to
write integers on slips of paper and place them in a hat.
Draw one slip at a time.
After each drawing replace the slip in the hat.
The probability of
drawing the integer i is given by the ratio ai of the number of slips
containing the integer i divided by the total number of slips.
Obviously the sum over i of ai must be unity.
Another way to get random integers
is to throw one of a pair of dice.
Then all ai equal zero except
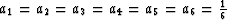 .The probability that the
integer i will occur on the first drawing and the integer j will
occur on the second drawing is ai aj.
If you draw two slips or throw a pair of dice,
then the probability that the sum of i and j equals k is
readily seen to be
.The probability that the
integer i will occur on the first drawing and the integer j will
occur on the second drawing is ai aj.
If you draw two slips or throw a pair of dice,
then the probability that the sum of i and j equals k is
readily seen to be
| 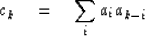 |
(53) |
Since this equation is a convolution, we may look into the meaning of the
Z transform
| 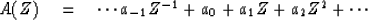 |
(54) |
In terms of Z transforms the probability that i plus j equals k is
simply the coefficient of Zk in
| 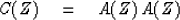 |
(55) |
Obviously,
if we add n of the random numbers,
the probability that the sum
of them equals k is given by the coefficient of Zk in
| ![\begin{displaymath}
G(Z) \eq [A(Z)]^n\end{displaymath}](img137.gif) |
(56) |
The central-limit theorem of probability says that as n does to infinity the
polynomial G(Z) goes to a special form,
almost regardless of the specific polynomial A(Z).
The specific form is such that a graph of the
coefficients of G(Z) comes closer and closer to fitting under the envelope
of the bell-shaped gaussian function.
Let us see why this happens.
Our development will lack a mathematical rigor
because the theorem is not always true.
There are pathological A functions which do not result in G
tending to gaussian.
Despite the fact that some of the pathological functions
sometimes turn up in applications,
we will not take the time here to look at such instances.
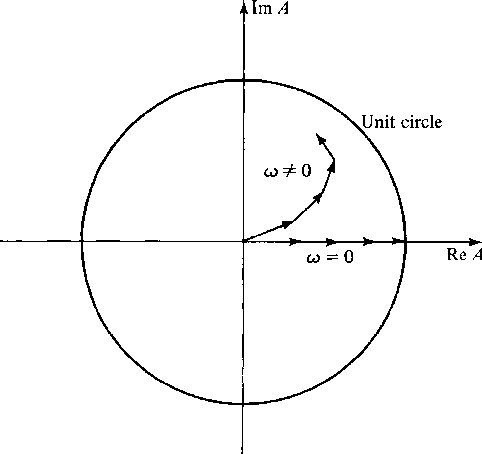
Consider the size of A(Z) for real 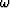 .If
.If 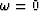 , the sum of the terms of A(Z)
may be visualized in the complex plane as a sum of vectors
, the sum of the terms of A(Z)
may be visualized in the complex plane as a sum of vectors
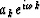 all pointing in the positive real direction.
If
all pointing in the positive real direction.
If 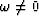 the vectors point in different directions.
This is shown in Figure 9.
the vectors point in different directions.
This is shown in Figure 9.
4-8
Figure 9 The complex numbers 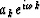 added together.
added together.
|
|  |

In raising 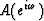 to the nth power,
the values of
to the nth power,
the values of 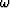 of greatest concern are those near
of greatest concern are those near 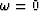 where A is
largest--because in any region where A is small
An will be extremely small.
Near
where A is
largest--because in any region where A is small
An will be extremely small.
Near 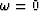 or Z = 1 we may expand A(Z)
in a power series in
or Z = 1 we may expand A(Z)
in a power series in 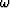
| 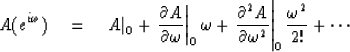 |
(57) |
Note that the coefficients of this power series are proportional to the moments
mi of the probability function; that is
| 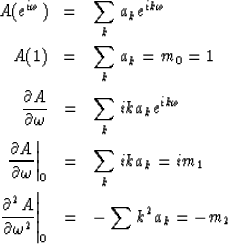 |
(58) |
| (59) |
| (60) |
| (61) |
| (62) |
When we raise A(Z) to the nth power we will make the conjecture that only
the given first three terms of the power series expansion will be important.
(This assumption clearly fails if any of the moments of the probability
function are infinite.)
Thus, we are saying that as far as G is concerned
the only important things about A are its mean value m = m1 and its
second moment m2.
If this is really so, we may calculate G by
replacing A with any function B having the same mean and same second
moment as A.
We may use the simplest function we can find. A good choice
is the so called binomial probability function given by
| 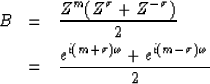 |
(63) |
| (64) |
Let us verify its first moment
| 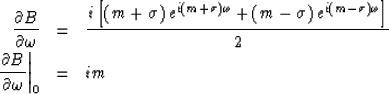 |
(65) |
| (66) |
Now let us verify its second moment
| 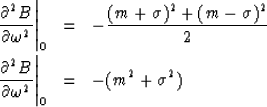 |
(67) |
| (68) |
Hence,  should be chosen so that
should be chosen so that
|  |
(69) |
Of course, we cannot expect that m and  will necessarily turn out
to be integers;
therefore (63) will not necessarily be a Z
transform in the usual sense.
It does not really matter;
we simply interpret
(63) as saying:
will necessarily turn out
to be integers;
therefore (63) will not necessarily be a Z
transform in the usual sense.
It does not really matter;
we simply interpret
(63) as saying:
- 1.
- The probability of drawing the number
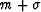 is one-half.
is one-half.
- 2.
- The probability of
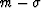 is one-half.
is one-half.
- 3.
- The probability of any other number is zero.
Now, raising 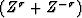 to the nth power gives
a series in powers of
to the nth power gives
a series in powers of 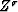 whose coefficients are symmetrically
distributed about Z to the zero power and whose magnitudes are given
by the binomial coefficients. A sketch of the coefficients of B(Z)n
is given in Figure 10.
whose coefficients are symmetrically
distributed about Z to the zero power and whose magnitudes are given
by the binomial coefficients. A sketch of the coefficients of B(Z)n
is given in Figure 10.
4-9
Figure 10 Coefficients of binomial raised to power

We will now see how, for large n, the binomial coefficients
asymptotically approach a gaussian.
Approaching this limit is a bit tricky.
Obviously, the sum of n random integers will diverge as 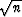 .Likewise the coefficients of powers of Z in
.Likewise the coefficients of powers of Z in
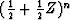 individually get smaller while the number of coefficients gets larger.
We recall that in time series analysis
we used th substitution
individually get smaller while the number of coefficients gets larger.
We recall that in time series analysis
we used th substitution 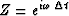 .We commonly chose
.We commonly chose 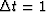 ,which had the meaning
that data points were given at integral points on the time axis.
In the
present probability theory application of Z transforms,
the choice
,which had the meaning
that data points were given at integral points on the time axis.
In the
present probability theory application of Z transforms,
the choice
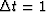 arises from our original statement that the numbers chosen
randomly from the slips of paper were integers.
Now we wish to add n
of these random numbers together;
and so, it makes sense to rescale the
integers to be integers divided by
arises from our original statement that the numbers chosen
randomly from the slips of paper were integers.
Now we wish to add n
of these random numbers together;
and so, it makes sense to rescale the
integers to be integers divided by 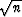 .Then we can make the
substitution
.Then we can make the
substitution 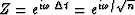 .The coefficient of Zk now refers to the probability of drawing the
number
.The coefficient of Zk now refers to the probability of drawing the
number 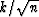 .Raising
.Raising 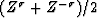 to the
nth power to find the probability distribution for the sum of n
to the
nth power to find the probability distribution for the sum of n
Using the first term of the series expansion for cosine we have
![\begin{displaymath}[B(Z)]
^n \approx \left( 1 - {\sigma^2 \omega^2 \over 2n} \right)^n\end{displaymath}](img159.gif)
Using the well-known fact that 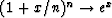 , we have for
large n
, we have for
large n
| ![\begin{displaymath}[B(Z)]
^n \approx e^{-\sigma^2 \omega^2/2}\end{displaymath}](img161.gif) |
(70) |
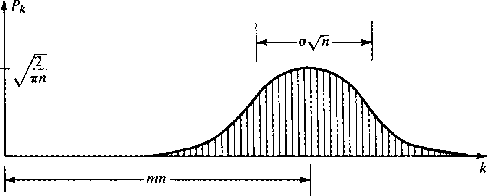
The probability that the number t will result from the sum is now found
by inverse Fourier transformation of (70).
The Fourier transform of
the gaussian (70) may be looked up in a table of integrals.
It is found to be the gaussian
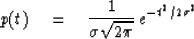





Next: CONFIDENCE INTERVALS
Up: Resolution
Previous: TIME-FREQUENCY-STATISTICAL RESOLUTION
Stanford Exploration Project
10/30/1997
![]() .The probability that the
integer i will occur on the first drawing and the integer j will
occur on the second drawing is ai aj.
If you draw two slips or throw a pair of dice,
then the probability that the sum of i and j equals k is
readily seen to be
.The probability that the
integer i will occur on the first drawing and the integer j will
occur on the second drawing is ai aj.
If you draw two slips or throw a pair of dice,
then the probability that the sum of i and j equals k is
readily seen to be
![]() .If
.If ![]() , the sum of the terms of A(Z)
may be visualized in the complex plane as a sum of vectors
, the sum of the terms of A(Z)
may be visualized in the complex plane as a sum of vectors
![]() all pointing in the positive real direction.
If
all pointing in the positive real direction.
If ![]() the vectors point in different directions.
This is shown in Figure 9.
the vectors point in different directions.
This is shown in Figure 9.

![]() to the nth power,
the values of
to the nth power,
the values of ![]() of greatest concern are those near
of greatest concern are those near ![]() where A is
largest--because in any region where A is small
An will be extremely small.
Near
where A is
largest--because in any region where A is small
An will be extremely small.
Near ![]() or Z = 1 we may expand A(Z)
in a power series in
or Z = 1 we may expand A(Z)
in a power series in ![]()
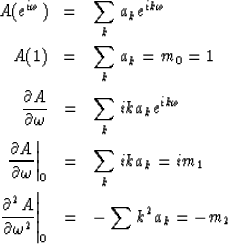
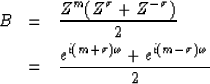
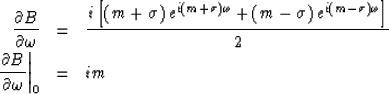
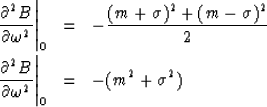
![]() to the nth power gives
a series in powers of
to the nth power gives
a series in powers of ![]() whose coefficients are symmetrically
distributed about Z to the zero power and whose magnitudes are given
by the binomial coefficients. A sketch of the coefficients of B(Z)n
is given in Figure 10.
whose coefficients are symmetrically
distributed about Z to the zero power and whose magnitudes are given
by the binomial coefficients. A sketch of the coefficients of B(Z)n
is given in Figure 10.
![]() .Likewise the coefficients of powers of Z in
.Likewise the coefficients of powers of Z in
![]() individually get smaller while the number of coefficients gets larger.
We recall that in time series analysis
we used th substitution
individually get smaller while the number of coefficients gets larger.
We recall that in time series analysis
we used th substitution ![]() .We commonly chose
.We commonly chose ![]() ,which had the meaning
that data points were given at integral points on the time axis.
In the
present probability theory application of Z transforms,
the choice
,which had the meaning
that data points were given at integral points on the time axis.
In the
present probability theory application of Z transforms,
the choice
![]() arises from our original statement that the numbers chosen
randomly from the slips of paper were integers.
Now we wish to add n
of these random numbers together;
and so, it makes sense to rescale the
integers to be integers divided by
arises from our original statement that the numbers chosen
randomly from the slips of paper were integers.
Now we wish to add n
of these random numbers together;
and so, it makes sense to rescale the
integers to be integers divided by ![]() .Then we can make the
substitution
.Then we can make the
substitution ![]() .The coefficient of Zk now refers to the probability of drawing the
number
.The coefficient of Zk now refers to the probability of drawing the
number ![]() .Raising
.Raising ![]() to the
nth power to find the probability distribution for the sum of n
to the
nth power to find the probability distribution for the sum of n
![\begin{eqnarraystar}[B(Z)]
^n &=& \left( {Z^{\sigma} + Z^{-\sigma} \over 2} \rig...
...&=& \left( {\cos {\sigma \omega \over \sqrt{n}}} \right)^n \\ \end{eqnarraystar}](img158.gif)
![]()
![]()