|
2-1
Figure 1 Sometimes the input to a filter is unknown. |  |
To understand causal filters better, we now take up the task of undoing what a causal filter has done. Consider the output yt of a filter bt is known but the input xt is unknown. See Figure 1.
|
2-1
Figure 1 Sometimes the input to a filter is unknown. |  |
This is the problem that one always has with a transducer/recorder system. For example, the output of a seismometer is a wiggly line on a piece of paper from which the seismologist may wish to determine the displacement, velocity, or acceleration of the ground. To undo the filtering operation of the filter B(Z), we will try to find another filter A(Z) as indicated in Figure 2.
|
2-2
Figure 2 The filter A(Z) is inverse to the filter B(Z). |
To solve for the coefficients of the filter A(Z), we merely identify coefficients of powers of Z in B(Z)A(Z) = 1. For B(Z), a three-term filter, this is
| |
(1) |
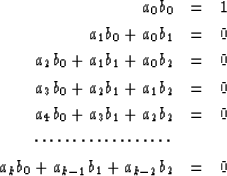 |
(2) | |
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
| (7) |
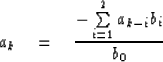 |
(8) |
Consider the example where B(Z) = 1 - Z/2; then, by equations like (2) to (7), by the binomial theorem, by polynomial division, or by Taylor's power series formula we obtain
| |
(9) |
| |
(10) |
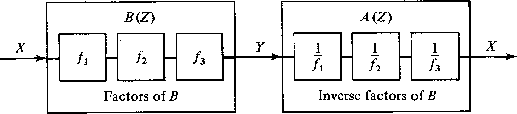 |
Recalling earlier discussion that a polynomial B(Z) of degree N may be factored into N subsystems and that the ordering of subsystems is unimportant (see Figure 3), we suspect that if any of the N roots of B(Z) lies inside the unit circle we may have difficulty with A(Z). Actual proof of this suspicion relies on a theorem from complex-variable theory about absolutely convergent series. The theorem is that the product of absolutely convergent series is convergent, and conversely the product of any convergent series with a divergent series is divergent. Another proof may be based upon the fact that a power series for 1/B(Z) converges in a circle about the origin with a radius from the origin out to he first pole [the zero of B(Z) of smallest magnitude]. Convergence of A(Z) on the unit circle means, in terms of filters, that the coefficients of A(Z) are decreasing. Thus, if all the zeros of B(Z) are outside the unit circle, we will get a convergent filter from (8).
Can anything at all be done if there is one root or more inside the circle? An answer is suggested by the example
| |
(11) |
In the general case, then, one must factor B(Z) into two parts: B(Z) = Bout(Z) Bin(Z) where Bout contains roots outside the unit circle and Bin contains the roots inside. Then the inverse of Bout is expressed as a Taylor series about the origin and the inverse of Bin is expressed as a Taylor series about infinity. The final expression for 1/B(Z) is called a Laurent expansion for 1/B(Z), and it converges on a ring surrounding the unit circle. Cases with zeros exactly on the unit circle present special problems. Sometimes you can argue yourself out of the difficulty but at other times roots on or even near the circle may mean that a certain computing scheme won't work out well in practice.
Finally, let us consider a mechanical interpretation. The stress (pressure) in a material may be represented by xt, and the strain (volume charge) may be represented by yt. The following two statements are equivalent; that is, in some situations they are both true, and in other situations they are both false:
STATEMENT A The stress in a material may be expressed as a linear combination of present and past strains. Likewise, the strain may be deduced from present and past stresses.
STATEMENT B The filter which relates stress to strain and vice versa has all poles and zeros outside the unit circle.