It is natural to begin studies of waves with equations that describe plane waves in a medium of constant velocity.
Figure 7 depicts a ray moving down into the earth
at an angle ![]() from the vertical.
from the vertical.
|
front
Figure 7 Downgoing ray and wavefront. | 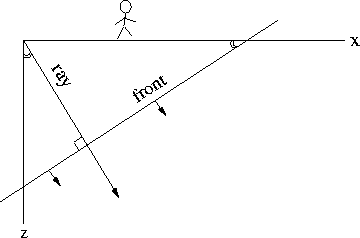 |
Perpendicular to the ray is a wavefront.
By elementary geometry the angle between the wavefront
and the earth's surface
is also ![]() .The ray increases its length at a speed v.
The speed that is observable on the earth's surface is the intercept
of the wavefront with the earth's surface.
This speed, namely
.The ray increases its length at a speed v.
The speed that is observable on the earth's surface is the intercept
of the wavefront with the earth's surface.
This speed, namely ![]() , is faster than v.
Likewise, the speed of the intercept of the wavefront and
the vertical axis is
, is faster than v.
Likewise, the speed of the intercept of the wavefront and
the vertical axis is ![]() .A mathematical expression for a straight line
like that shown to be the wavefront in Figure 7 is
.A mathematical expression for a straight line
like that shown to be the wavefront in Figure 7 is
| |
(4) |
In this expression z0 is the intercept between the wavefront and the vertical axis. To make the intercept move downward, replace it by the appropriate velocity times time:
| |
(5) |
| |
(6) |
| |
(7) |