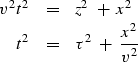
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
 |
(8) | |
| (9) |
A seismic trace is a signal d(t)
recorded at some constant x.
We can convert the trace
to a ``vertical propagation'' signal
![]() by stretching t to
by stretching t to ![]() .This process is called
``normal moveout correction'' (NMO).
Typically we have many traces at different x distances
each of which theoretically produces the same
hypothetical zero-offset trace.
Figure 1 shows a marine shot profile
before and after NMO correction at the water velocity.
You can notice that the wave packet reflected from the ocean bottom
is approximately a constant width on the raw data.
After NMO, however,
this waveform broadens considerably--a phenomenon known
as ``NMO stretch."
.This process is called
``normal moveout correction'' (NMO).
Typically we have many traces at different x distances
each of which theoretically produces the same
hypothetical zero-offset trace.
Figure 1 shows a marine shot profile
before and after NMO correction at the water velocity.
You can notice that the wave packet reflected from the ocean bottom
is approximately a constant width on the raw data.
After NMO, however,
this waveform broadens considerably--a phenomenon known
as ``NMO stretch."
|
stretch
Figure 1 Marine data moved out with water velocity. Input on the left, output on the right. Press button for movie sweeping through velocity (actually through slowness squared). |  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
The NMO transformation ![]() is representable as a square matrix.
The matrix
is representable as a square matrix.
The matrix ![]() is a
is a ![]() -plane containing all zeros
except an interpolation operator centered along the hyperbola.
The dots in the matrix below are zeros.
The input signal dt is put into the vector
-plane containing all zeros
except an interpolation operator centered along the hyperbola.
The dots in the matrix below are zeros.
The input signal dt is put into the vector ![]() .The output vector
.The output vector ![]() --i.e., the NMO'ed signal--is simply
(d6,d6,d6, d7,d7, d8,d8, d9, d10, 0).
In real life examples such as Figure 1
the subscript goes up to about one thousand instead of
merely to ten.
--i.e., the NMO'ed signal--is simply
(d6,d6,d6, d7,d7, d8,d8, d9, d10, 0).
In real life examples such as Figure 1
the subscript goes up to about one thousand instead of
merely to ten.
![\begin{displaymath}
{\bf m\eq Nd} \eq
\left[
\begin{array}
{c}
m_1 \\
m_2...
...\ d_6 \\ d_7 \\ d_8 \\ d_9 \\ d_{10}
\end{array} \right] \end{displaymath}](img24.gif) |
(10) |
You can think of the matrix as having a horizontal t-axis and
a vertical ![]() -axis.
The 1's in the matrix are arranged on the hyperbola
-axis.
The 1's in the matrix are arranged on the hyperbola
![]() .The transpose matrix defining some
.The transpose matrix defining some ![]() from
from ![]() gives synthetic data
gives synthetic data ![]() from the zero-offset
(or stack) model
from the zero-offset
(or stack) model ![]() , namely,
, namely,
![\begin{displaymath}
{\bf \tilde d \eq N' m } \eq
\left[
\begin{array}
{c}
\t...
...\\ m_6 \\ m_7 \\ m_8 \\ m_9 \\ m_{10}
\end{array} \right]\end{displaymath}](img27.gif) |
(11) |
A program for nearest-neighbor normal moveout as defined by
equations (10) and (11)
is nmo0().
Because of the limited alphabet of programming languages,
I used the keystroke z to denote ![]() .
.
subroutine nmo0( adj, add, slow, x, t0, dt, n,zz, tt )
integer it, iz, adj, add, n
real xs, t , z, slow(n), x, t0, dt, zz(n), tt(n)
call adjnull( adj, add, zz,n, tt,n)
do iz= 1, n { z = t0 + dt*(iz-1) # Travel-time depth
xs= x * slow(iz)
t = sqrt ( z * z + xs * xs)
it= 1 + .5 + (t - t0) / dt # Round to nearest neighbor.
if( it <= n )
if( adj == 0 )
tt(it) = tt(it) + zz(iz)
else
zz(iz) = zz(iz) + tt(it)
}
return; end
A program is a ``pull'' program if the loop creating the output
covers each location in the output and gathers the input from wherever
it may be.
A program is a ``push'' program if it takes each input and
pushes it to wherever it belongs.
Thus this NMO program is a ``pull'' program
for doing the model building (data processing),
and it is a ``push'' program for the data building.
You could write a program that worked the other way around,
namely, a loop over t with z found
by calculation ![]() .What is annoying is that if you want a push program going
both ways, those two ways cannot be adjoint to one another.
.What is annoying is that if you want a push program going
both ways, those two ways cannot be adjoint to one another.
Normal moveout is a linear operation.
This means that data can be decomposed into any two parts,
early and late,
high frequency and low,
smooth and rough,
steep and shallow dip, etc.;
and whether the two parts
are NMO'ed either separately or together, the result is the same.
The reason normal moveout is a linear operation
is that we have shown it is effectively a matrix multiply operation
and that operation fulfills ![]() .
.