Velocity picking

For many kinds of data analysis, we need to know the velocity of the earth as a function of depth. To derive such information we begin from Figure 9 and draw a line through the maxima. In practice this is often a tedious manual process, and it needs to be done everywhere we go. There is no universally accepted way to automate this procedure, but we will consider one that is simple enough that it can be fully described here, and which works well enough for these demonstrations. (I plan to do a better job later.)

Theoretically we can define the velocity or slowness as a function of traveltime depth by the moment function. Take the absolute value of the data scans and smooth them a little on the time axis to make something like an unnormalized probability function, say $p(\tau ,s)\gt$.Then the slowness $s(\tau )$ could be defined by the moment function, i.e.,  

$$s(\tau ) \eq { \sum_s \ s\ p(\tau ,s) \over \sum_s \ p(\tau ,s) }$$ (12)

The problem with defining slowness $s(\tau )$ by the moment is that it is strongly influenced by noises away from the peaks, particularly water velocity noises. Thus, better results can be obtained if the sums in equation (12) are limited to a range about the likely solution. To begin with, we can take the likely solution to be defined by universal or regional experience. It is sensible to begin from a one-parameter equation for velocity increasing with depth where the form of the equation allows a ray tracing solution such as equation (). 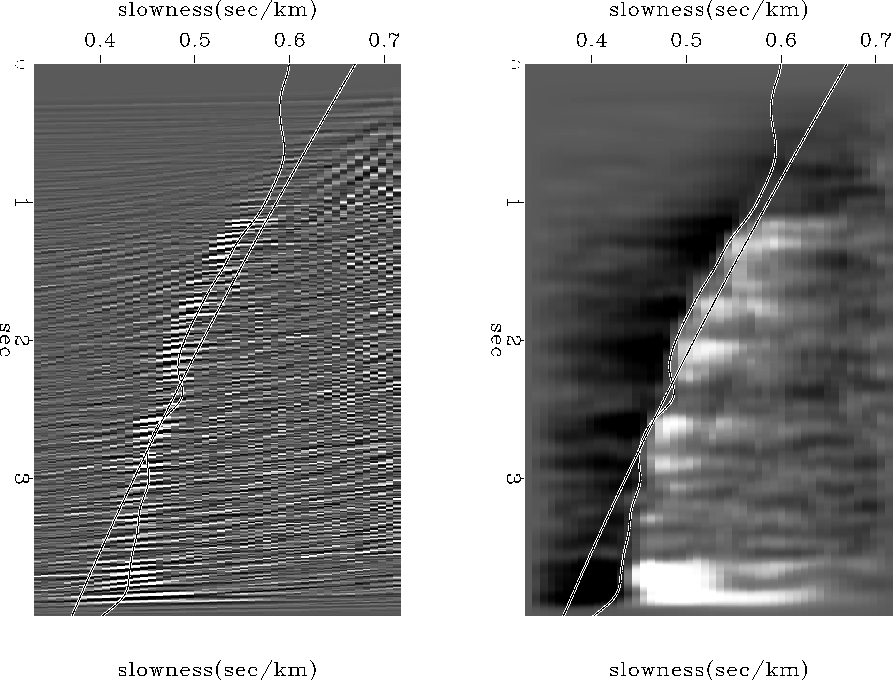Experience with Gulf of Mexico data shows that $\alpha\approx 1/2\ {\rm sec}^{-1}$ is reasonable there for equation (), and that is the smooth curve in Figure 10.

Experience with moments, equation (12), shows they are reasonable when the desired result is near the guessed center of the range. Otherwise, the moment is biased towards the initial guess. This bias can be reduced in stages. At each stage we shrink the width of the zone used to compute the moment. This procedure is used in subroutine slowfit() which after smoothing to be described, gives the oscillatory curve you see in Figure 10.

 

subroutine slowfit( vsurface, alpha, t0,dt, s0,ds, scan,nt,ns, reg,    slow)
integer irange, it,is,                                  nt,ns
real num,den, t,s,  vsurface, alpha, t0,dt, s0,ds, scan(nt,ns),reg(nt),slow(nt)
do it= 1, nt {  t= t0 + dt*(it-1) + dt
        reg(it)  = 1./( vsurface * sqrt( (exp(alpha*t) - 1.)/(alpha*t) ))
        slow(it) = reg(it)
        }
do irange= ns/4, 5, -1 {                                # shrink the fairway
do it=     1,   nt     {        t= t0 + dt*(it-1)
        do is= 1, ns   {        s= s0 + ds*(is-1)
                if( s > slow(it) + irange*ds)   scan(it,is) = 0.
                if( s < slow(it) - irange*ds)   scan(it,is) = 0.
                if( s > 1./1.6              )   scan(it,is) = 0.        # water
                }
        den= 0.0;       num= 0.0
        do is= 1, ns {  s= s0 + ds*(is-1)
                num = num + scan(it,is) * s
                den = den + scan(it,is)
                }
        slow(it) = num / ( den + 1.e-20)
        if( slow(it) == 0.)   slow(it) = 1./vsurface
        }}
return; end

A more customary way to view velocity space is to square the velocity scans and normalize them by the sum of the squares of the signals. This has the advantage that the remaining information represents velocity spectra and removes variation due to seismic amplitudes. Since in practice, reliability seems somehow proportional to amplitude the disadvantage of normalization is that reliability becomes more veiled.

An appealing visualization of velocity is shown in the right side of Figure 10. This was prepared from the absolute value of left side, followed by filtering spatially with an antisymmetric leaky integral function. (See PVI page 57). An example is shown on the right side of Figure 10.

 

slowfit
Figure 10 Left is the slowness scans. Right is the slowness scans after absolute value, smoothing a little in time, and antisymmetric leaky integration over slowness. Overlaying both is the line of slowness picks.