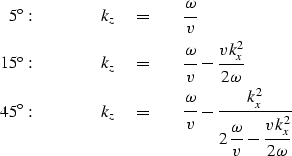
Substituting the definitions (60) into equation (65) et. seq. gives dispersion relationships for comparison to the exact expression (59).
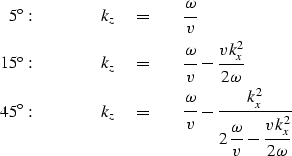 |
(65) | |
Identification of i kz with ![]() converts
the dispersion relations (65)
into the differential equations
converts
the dispersion relations (65)
into the differential equations
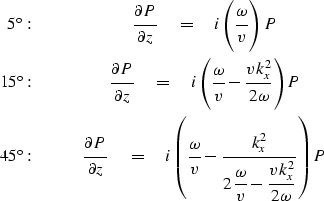 |
(66) | |
The differential equations above
in Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4
were based on a dispersion relation
that in turn was based on an assumption of constant velocity.
Surprisingly, these equations also have validity and great utility
when the velocity is depth-variable, v = v(z).
The limitation is that the velocity be constant over each
depth ``slab'' of width
.4
were based on a dispersion relation
that in turn was based on an assumption of constant velocity.
Surprisingly, these equations also have validity and great utility
when the velocity is depth-variable, v = v(z).
The limitation is that the velocity be constant over each
depth ``slab'' of width ![]() over which the downward-continuation
is carried out.
over which the downward-continuation
is carried out.